- Quiz will start as soon as you click the ‘Start Quiz‘ button below.
- Question will come one by one click on next for next question
- There are 30 questions in this quiz, you will get 30 Minutes to attempt.
- 2 Marks is determined for the correct answer for each question. There is no negative marking for incorrect answer.
- After the quiz is over, in order to know your rank in the Ranking List / Leader-board below, you should enter your name and email address, otherwise you will be deprived of it.
- After completing click on finish Quiz
- To see correct answers click on view Question
- जैसे ही आप नीचे दिए गए ‘स्टार्ट क्विज़’ बटन पर क्लिक करेंगे, क्विज़ शुरू हो जाएगा।
प्रश्न अगले प्रश्न के लिए अगले एक क्लिक पर आएगा
इस क्विज में 30 प्रश्न हैं, आपको प्रयास करने के लिए 30 मिनट मिलेंगे।
प्रत्येक प्रश्न के सही उत्तर के लिए 2 अंक निर्धारित किए गए हैं। गलत उत्तर के लिए कोई नकारात्मक अंकन नहीं है।
प्रश्नोत्तरी समाप्त होने के बाद, नीचे दी गई रैंकिंग सूची / लीडर-बोर्ड में अपनी रैंक जानने के लिए, आपको अपना नाम और ईमेल पता दर्ज करना चाहिए, अन्यथा आप इससे वंचित रह जाएंगे।
फिनिश क्विज़ पर क्लिक करने के बाद
सही उत्तर देखने के लिए प्रश्न पर क्लिक करें
Paper 2 CS Discrete Structures and Optimization Part 4
Quiz-summary
0 of 30 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
Information
Paper 1 Quiz helps u to Excel in NET JRF
Paper 1 All questions 2 Marks each
- Navdeep Kaur
- All the Best
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Results
0 of 30 questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 points, (0)
| Average score |
|
| Your score |
|
Categories
- Not categorized 0%
-
Average marks Improve next time All the Best
-
Nice Keep it up, Stay Blessed
-
Awesome Great Marks, Keep doing
| Pos. | Name | Entered on | Points | Result |
|---|---|---|---|---|
| Table is loading | ||||
| No data available | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- Answered
- Review
-
Question 1 of 30
1. Question
2 pointsConsider a Hamiltonian Graph G with no loops or parallel edges and with |V(G)| = n ≥ 3. Then which of the following is true ?
Correct
With the help of dirac’s theorem, we can prove above three statements.
Incorrect
With the help of dirac’s theorem, we can prove above three statements.
-
Question 2 of 30
2. Question
2 points“How many multiples of 6 are there between the following pairs of numbers ?
0 and 100 and –6 and 34”Correct
“0 and 100 → Counting sequentially:
0,6,12,18,24,30,36,42,48,54,60,66,72,78,84,90,96 Total=17
–6 and 34 → Counting sequentially: -6,0,6,12,18,24,30
Total=7 “Incorrect
“0 and 100 → Counting sequentially:
0,6,12,18,24,30,36,42,48,54,60,66,72,78,84,90,96 Total=17
–6 and 34 → Counting sequentially: -6,0,6,12,18,24,30
Total=7 “ -
Question 3 of 30
3. Question
2 pointsThe functions mapping R into R are defined as : f(x) = x 3 – 4x, g(x) = 1/(x 2 + 1) and h(x) = x 4 . Then find the value of the following composite functions : hog(x) and hogof(x)
Correct
“Step-1: Given data,
f(x) = x^3 – 4x, g(x) = 1/(x^ 2 + 1) and h(x) = x ^4
hog(x)=h(1/(x ^2 + 1))
=h(1/(x ^2 )+1)^ 4
= 1/(x^ 2 +1)^ 4
= (x ^2 +1) ^-4
hogof(x)= hog(x^ 3 -4x)
= h(1/(x^ 3 -4x)^ 2 +1)
= h(1/(x^ 3 -4x)^ 2 +1)^ 4
= h((x^ 3 -4x)^ 2 +1)^ -4
So, option D id is correct answer. “Incorrect
“Step-1: Given data,
f(x) = x^3 – 4x, g(x) = 1/(x^ 2 + 1) and h(x) = x ^4
hog(x)=h(1/(x ^2 + 1))
=h(1/(x ^2 )+1)^ 4
= 1/(x^ 2 +1)^ 4
= (x ^2 +1) ^-4
hogof(x)= hog(x^ 3 -4x)
= h(1/(x^ 3 -4x)^ 2 +1)
= h(1/(x^ 3 -4x)^ 2 +1)^ 4
= h((x^ 3 -4x)^ 2 +1)^ -4
So, option D id is correct answer. “ -
Question 4 of 30
4. Question
2 points“Consider a sequence F 00 defined as : F 00 (0) = 1, F 00 (1) = 1
F 00 (n) = ((10 ∗ F 00 (n – 1) + 100)/ F 00 (n – 2)) for n ≥ 2 Then what shall be the set of values of the sequence F 00 ?”Correct
“Given data,
Sequence F 00 defined as
F 00 (0) = 1,
F 00 (1) = 1,
F 00 (n) = ((10 ∗ F 00 (n – 1) + 100)/ F 00 (n – 2)) for n ≥ 2
Let n=2
F 00 (2) = (10 * F 00 (1) + 100) / F 00 (2 – 2)
= (10 * 1 + 100) / 1
= (10 + 100) / 1
= 110
Let n=3
F 00 (3) = (10 * F 00 (2) + 100) / F 00 (3 – 2)
= (10 * 110 + 100) / 1
= (1100 + 100) / 1
= 1200
Similarly, n=4
F 00 (4) = (10 * F 00 (3) + 100) / F 00 (4 – 2)
= (12100) / 110
= 110
F 00 (5) = (10 * F 00 (4) + 100) / F 00 (5 – 2)
= (10*110 + 100) / 1200
= 1
The sequence will be (1, 110, 1200,110, 1). “Incorrect
“Given data,
Sequence F 00 defined as
F 00 (0) = 1,
F 00 (1) = 1,
F 00 (n) = ((10 ∗ F 00 (n – 1) + 100)/ F 00 (n – 2)) for n ≥ 2
Let n=2
F 00 (2) = (10 * F 00 (1) + 100) / F 00 (2 – 2)
= (10 * 1 + 100) / 1
= (10 + 100) / 1
= 110
Let n=3
F 00 (3) = (10 * F 00 (2) + 100) / F 00 (3 – 2)
= (10 * 110 + 100) / 1
= (1100 + 100) / 1
= 1200
Similarly, n=4
F 00 (4) = (10 * F 00 (3) + 100) / F 00 (4 – 2)
= (12100) / 110
= 110
F 00 (5) = (10 * F 00 (4) + 100) / F 00 (5 – 2)
= (10*110 + 100) / 1200
= 1
The sequence will be (1, 110, 1200,110, 1). “ -
Question 5 of 30
5. Question
2 pointsNegation of the proposition ∃x H(x) is:
Correct
Take negation inside.
Incorrect
Take negation inside.
-
Question 6 of 30
6. Question
2 points“Let P and Q be two propositions, ¬ (P ↔ Q) is equivalent to:
(I) P ↔ ¬ Q
(II) ¬ P ↔ Q
(III) ¬ P ↔ ¬ Q
(IV) Q → P “Correct
 Incorrect
Incorrect

-
Question 7 of 30
7. Question
2 points“How many distinguishable permutations of the letters in the word BANANA are there ?
Correct
“Total distinguishable permutations means no repetition.
BANANA= 6 letters
B is appearing 1 time
A is appearing 3 times
N is appearing 2 times
So, = 6! / (3! * 2!)
= 60 “Incorrect
“Total distinguishable permutations means no repetition.
BANANA= 6 letters
B is appearing 1 time
A is appearing 3 times
N is appearing 2 times
So, = 6! / (3! * 2!)
= 60 “ -
Question 8 of 30
8. Question
2 pointsThe sum of the series: (1/2) + (1/3) + (1/4) – (1/6) + (1/8) + (1/9) + (1/16) – (1/12) + … + α is:
Correct
The sum of the series: (1/2) + (1/3) + (1/4) – (1/6) + (1/8) + (1/9) + (1/16) – (1/12) + … + α is 1 + log(√2)3.
Incorrect
The sum of the series: (1/2) + (1/3) + (1/4) – (1/6) + (1/8) + (1/9) + (1/16) – (1/12) + … + α is 1 + log(√2)3.
-
Question 9 of 30
9. Question
2 pointsIf a lattice (L,R) has a greatest and least element then it is said to be:
Correct
“→ In a Lattice if Upper Bound and Lower exists then it is called Bounded Lattice.
→ A bounded lattice is an algebraic structure of the form (L, ∨, ∧, 0, 1) such that (L, ∨, ∧) is a lattice, 0 (the lattice’s bottom) is the identity element for the join operation ∨, and 1 (the lattice top) is the identity element for the meet operation ∧.
→ Let ‘L’ be a lattice w.r.t R if there exists an element I∈L such that (aRI)∀x∈L, then I is called Upper Bound of a Lattice L.
Similarly, if there exists an element O∈L such that (ORa)∀a∈L, then O is called Lower Bound of Lattice L. “Incorrect
“→ In a Lattice if Upper Bound and Lower exists then it is called Bounded Lattice.
→ A bounded lattice is an algebraic structure of the form (L, ∨, ∧, 0, 1) such that (L, ∨, ∧) is a lattice, 0 (the lattice’s bottom) is the identity element for the join operation ∨, and 1 (the lattice top) is the identity element for the meet operation ∧.
→ Let ‘L’ be a lattice w.r.t R if there exists an element I∈L such that (aRI)∀x∈L, then I is called Upper Bound of a Lattice L.
Similarly, if there exists an element O∈L such that (ORa)∀a∈L, then O is called Lower Bound of Lattice L. “ -
Question 10 of 30
10. Question
2 pointsIf a relation < from A={1,2,3,4} to B={1,3,5} i.e., (a,b)∈R if a < b, then R-1 is:
Correct
The relation R is {(1,3), (1,5),(2,3),(2,5),(3,5),(4,5) } where (a,b) ∈ R if a The R-1 is { (3,1),(5,1),(3,2),(5,2),(5,3),(5,4) } where (a,b) ∈ R-1 if a>b.
Incorrect
The relation R is {(1,3), (1,5),(2,3),(2,5),(3,5),(4,5) } where (a,b) ∈ R if a The R-1 is { (3,1),(5,1),(3,2),(5,2),(5,3),(5,4) } where (a,b) ∈ R-1 if a>b.
-
Question 11 of 30
11. Question
2 pointsThe number of two digit numbers divisible by the product of digits is:
Correct
“11=1*1=1 which is a factor of 11
12=1*2=2 which is a factor of 12
15=1*5=5 which is a factor of 15
24=2*4=8 which is a factor of 24
36=3*6=12 which is a factor of 36 “Incorrect
“11=1*1=1 which is a factor of 11
12=1*2=2 which is a factor of 12
15=1*5=5 which is a factor of 15
24=2*4=8 which is a factor of 24
36=3*6=12 which is a factor of 36 “ -
Question 12 of 30
12. Question
2 pointsIn algebra of logic, the conjunction of two tautologies is:
Correct
“Some properties are tautologies:
1. The negation of a contradiction is a tautology.
2. The disjunction of two contingencies can be a tautology.
3. The conjunction of two tautologies is a tautology. “Incorrect
“Some properties are tautologies:
1. The negation of a contradiction is a tautology.
2. The disjunction of two contingencies can be a tautology.
3. The conjunction of two tautologies is a tautology. “ -
Question 13 of 30
13. Question
2 pointsHow many integers are between 1 and 200 which are divisible by any one of the integers 2,3 and 5(Hint: use set operation)?
Correct
“A) numbers divisible by 2: 200/2 = 100
B) numbers divisible by 3: 200/3 = 66
C) numbers divisible by 5: 200/5 = 40
Counting twice:
AB) numbers divisible by 6: 200/6 = 33
AC) numbers divisible by 10: 200/10 = 20
BC) numbers divisible by 15: 200/15 = 13
Counting 3 times:
ABC) numbers divisible by 30: 200/30 = 6
Total of numbers = A + B + C – AB – AC – BC + ABC = 100 + 66 + 40 – 33 – 20 -13 + 6 = 146 “Incorrect
“A) numbers divisible by 2: 200/2 = 100
B) numbers divisible by 3: 200/3 = 66
C) numbers divisible by 5: 200/5 = 40
Counting twice:
AB) numbers divisible by 6: 200/6 = 33
AC) numbers divisible by 10: 200/10 = 20
BC) numbers divisible by 15: 200/15 = 13
Counting 3 times:
ABC) numbers divisible by 30: 200/30 = 6
Total of numbers = A + B + C – AB – AC – BC + ABC = 100 + 66 + 40 – 33 – 20 -13 + 6 = 146 “ -
Question 14 of 30
14. Question
2 pointsThe sum of n terms of 1/(1*2) + 1/(2*3) + 1/(3*4) + … is
Correct
“Sum upto n terms = 1/(1*2) + 1/(2*3) + 1/(3*4) + …….. + 1/(n*(n+1))
where
1st term = 1/(1*2)
2nd term = 1/(2*3)
3rd term = 1/(3*4)
.
.
.
.
n-th term = 1/(n*(n+1))
n-th term = 1/(n*(n+1))
i.e. the k-th term is of the form 1/(k*(k+1))
which can further be written as k-th term = 1/k – 1/(k+1)
So, sum upto n terms can be calculated as:
(1/1 – 1/1+1) + (1/2 – 1/2+1) + (1/3 – 1/3+1) + ……… + (1/n-1 – /1n) + (1/n – 1/n+1)
= (1 – 1/2) + (1/2 – 1/3) + (1/3 – 1/4) + ……… + (1/n-1 – 1/n) + (1/n – 1/n+1)
= 1 – 1/n+1
= ((n+1) – 1)/n+1
= n/n+1 “Incorrect
“Sum upto n terms = 1/(1*2) + 1/(2*3) + 1/(3*4) + …….. + 1/(n*(n+1))
where
1st term = 1/(1*2)
2nd term = 1/(2*3)
3rd term = 1/(3*4)
.
.
.
.
n-th term = 1/(n*(n+1))
n-th term = 1/(n*(n+1))
i.e. the k-th term is of the form 1/(k*(k+1))
which can further be written as k-th term = 1/k – 1/(k+1)
So, sum upto n terms can be calculated as:
(1/1 – 1/1+1) + (1/2 – 1/2+1) + (1/3 – 1/3+1) + ……… + (1/n-1 – /1n) + (1/n – 1/n+1)
= (1 – 1/2) + (1/2 – 1/3) + (1/3 – 1/4) + ……… + (1/n-1 – 1/n) + (1/n – 1/n+1)
= 1 – 1/n+1
= ((n+1) – 1)/n+1
= n/n+1 “ -
Question 15 of 30
15. Question
2 pointsA declarative sentence which is either true(1) or false(0) is called:
Correct
“• Declarative sentences are propositions.
• Sentences that assert a fact that could either be true or false. “Incorrect
“• Declarative sentences are propositions.
• Sentences that assert a fact that could either be true or false. “ -
Question 16 of 30
16. Question
2 pointsRank of nonsingular square matrix of order r is:
Correct
“• A square matrix of order ’r’ is nonsingular if its determinant is non zero and therefore its rank is “r”. It’s all rows and columns are linearly independent and it is invertible.
• Rank of singular matrix is less than “r”. “Incorrect
“• A square matrix of order ’r’ is nonsingular if its determinant is non zero and therefore its rank is “r”. It’s all rows and columns are linearly independent and it is invertible.
• Rank of singular matrix is less than “r”. “ -
Question 17 of 30
17. Question
2 pointsA minimal subgraph G’ of G such that V(G’)=V(G) and G’ is connected is called:
Correct
Given a connected graph G, a connected subgraph that is both a tree and contains all the vertices of G is called a spanning tree for G.Given a connected graph G, a connected subgraph that is both a tree and contains all the vertices of G is called a spanning tree for G.
Incorrect
Given a connected graph G, a connected subgraph that is both a tree and contains all the vertices of G is called a spanning tree for G.
-
Question 18 of 30
18. Question
2 pointsIf k parallel lines of a determinant Δ become identical when x=a, then ____ is a factor of Δ.
Correct
“• If a determinant D vanishes for x = a, then (x – a) is a factor of D, in other words, if two rows (or two columns) become identical for x = a, then (x-a) is a factor of D.
• In general, if k rows (or k columns) become identical (x=a) when a is substituted for x, then (x-a)r-1 is a factor of D. “Incorrect
“• If a determinant D vanishes for x = a, then (x – a) is a factor of D, in other words, if two rows (or two columns) become identical for x = a, then (x-a) is a factor of D.
• In general, if k rows (or k columns) become identical (x=a) when a is substituted for x, then (x-a)r-1 is a factor of D. “ -
Question 19 of 30
19. Question
2 pointsIn how many ways can a committee of 4 people be chosen from a group of 12?
Correct
“As the order of people does not matter, it is C4 12
C(n,r) = C(12,4)
= 12! / [(4!(12−4)!)]
= 495
Hence, a committee of 4 people be selected from a group of 12 people in 495 ways. “Incorrect
“As the order of people does not matter, it is C4 12
C(n,r) = C(12,4)
= 12! / [(4!(12−4)!)]
= 495
Hence, a committee of 4 people be selected from a group of 12 people in 495 ways. “ -
Question 20 of 30
20. Question
2 pointsHow many 3 digit numbers are there with all different odd digits?
Correct
“• Three digit odd numbers implies the numbers would only be made of digits 1 , 3 , 5 , 7 , 9 With repetition of digits we would have had 5 * 5 * 5 = 125
• But for every hundreds, maximum of 4 tens is possible (avoiding the duplicate of digit used in hundreds)
• And each of these 4 tens, maximum of 3 units is possible (avoiding the duplicate of digits used in tens)
• 5 * 4 * 3 = 60 “Incorrect
“• Three digit odd numbers implies the numbers would only be made of digits 1 , 3 , 5 , 7 , 9 With repetition of digits we would have had 5 * 5 * 5 = 125
• But for every hundreds, maximum of 4 tens is possible (avoiding the duplicate of digit used in hundreds)
• And each of these 4 tens, maximum of 3 units is possible (avoiding the duplicate of digits used in tens)
• 5 * 4 * 3 = 60 “ -
Question 21 of 30
21. Question
2 pointsThe root mean square deviation when measured from the mean is:
Correct
The root mean square deviation when measured from the mean is least value.
Incorrect
The root mean square deviation when measured from the mean is least value.
-
Question 22 of 30
22. Question
2 pointsThe mean, mode and median are connected by the empirical relationship:
Correct
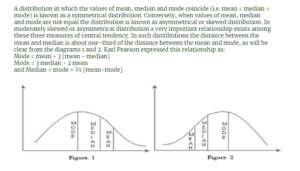 Incorrect
Incorrect

-
Question 23 of 30
23. Question
2 pointsThe algebraic sum of the deviations of all the variables from their mean is
Correct
The sum of the deviations from the mean is zero. This will always be the case as it is a property of the sample mean, i.e., the sum of the deviations below the mean will always equal the sum of the deviations above the mean. However, the goal is to capture the magnitude of these deviations in a summary measure.
Incorrect
The sum of the deviations from the mean is zero. This will always be the case as it is a property of the sample mean, i.e., the sum of the deviations below the mean will always equal the sum of the deviations above the mean. However, the goal is to capture the magnitude of these deviations in a summary measure.
-
Question 24 of 30
24. Question
2 pointsExponential distribution is special case of ____ distribution.
Correct
The exponential distribution is not the same as the class of exponential families of distributions, which is a large class of probability distributions that includes the exponential distribution as one of its members, but also includes the normal distribution, binomial distribution, gamma distribution, Poisson, and many others.
Incorrect
The exponential distribution is not the same as the class of exponential families of distributions, which is a large class of probability distributions that includes the exponential distribution as one of its members, but also includes the normal distribution, binomial distribution, gamma distribution, Poisson, and many others.
-
Question 25 of 30
25. Question
2 pointsThe normal curve is symmetrical about its:
Correct
Symmetrical distribution occurs when the values of variables occur at regular frequencies and the mean, median and mode occur at the same point. In graph form, symmetrical distribution often appears as a bell curve. If a line were drawn dissecting the middle of the graph, it would show two sides that mirror each other.
Incorrect
Symmetrical distribution occurs when the values of variables occur at regular frequencies and the mean, median and mode occur at the same point. In graph form, symmetrical distribution often appears as a bell curve. If a line were drawn dissecting the middle of the graph, it would show two sides that mirror each other.
-
Question 26 of 30
26. Question
2 pointsThe standard deviation of binomial distribution with n observations and probability of success p, probability of failure is q is:
Correct
 Incorrect
Incorrect

-
Question 27 of 30
27. Question
2 pointsIf the mean of a poisson distribution is m, then standard deviation of the distribution is:
Correct
Standard formula
Incorrect
Standard formula
-
Question 28 of 30
28. Question
2 pointsIf a random variable takes a finite set of values it is called:
Correct
“→ A discrete variable is a variable whose value is obtained by counting.
Examples:
number of students present
number of red marbles in a jar
number of heads when flipping three coins
students’ grade level
→ A discrete random variable X has a countable number of possible values.
Example:
Let X represent the sum of two dice.
→ A discrete random variable is one which may take on only a countable number of distinct values such as 0,1,2,3,4,…….. Discrete random variables are usually (but not necessarily) counts. If a random variable can take only a finite number of distinct values, then it must be discrete.
Examples of discrete random variables include the number of children in a family, the Friday night attendance at a cinema, the number of patients in a doctor’s surgery, the number of defective light bulbs in a box of ten. “Incorrect
“→ A discrete variable is a variable whose value is obtained by counting.
Examples:
number of students present
number of red marbles in a jar
number of heads when flipping three coins
students’ grade level
→ A discrete random variable X has a countable number of possible values.
Example:
Let X represent the sum of two dice.
→ A discrete random variable is one which may take on only a countable number of distinct values such as 0,1,2,3,4,…….. Discrete random variables are usually (but not necessarily) counts. If a random variable can take only a finite number of distinct values, then it must be discrete.
Examples of discrete random variables include the number of children in a family, the Friday night attendance at a cinema, the number of patients in a doctor’s surgery, the number of defective light bulbs in a box of ten. “ -
Question 29 of 30
29. Question
2 pointsM is a square matrix of order ‘n’ and its determinant value is 5. If all the elements of M are multiplied by 2, Its determinant value becomes 40. The value of ‘n’ is
Correct
“● From the matrix property : If each element of a row (or a column) of a determinant is multiplied by a constant k, then its value gets multiplied by k.
● Consider matrix order is 3, there are 3 rows and each row is multiplied by 2 means we need to multiply 8 to the existing determinant.
● The given existing determinant is 5 and each row multiplied by 2 means 8 *5 =40. “Incorrect
“● From the matrix property : If each element of a row (or a column) of a determinant is multiplied by a constant k, then its value gets multiplied by k.
● Consider matrix order is 3, there are 3 rows and each row is multiplied by 2 means we need to multiply 8 to the existing determinant.
● The given existing determinant is 5 and each row multiplied by 2 means 8 *5 =40. “ -
Question 30 of 30
30. Question
2 pointsThe solution of the recurrence relation a r =a r-1 +2a r-2 with a 0 =2,a 1 =7
Correct
“● Given the recurrence relation a r =a r-1 +2a r-2 and a 0 =2,a 1 =7.
● For r =2, a 2= a 2-1 +2a 2-2 =a 1 +2a 0 =7+2*2=7+4=11 ● For r=3,a 3= a 3-1 +2a 3-2 =a 2 +2a 1 =11+2*7=11+14=25
● From the above options ,Substitute the r values 0,1,2,3 then option -D gives the solution to recurrence relation. “Incorrect
“● Given the recurrence relation a r =a r-1 +2a r-2 and a 0 =2,a 1 =7.
● For r =2, a 2= a 2-1 +2a 2-2 =a 1 +2a 0 =7+2*2=7+4=11 ● For r=3,a 3= a 3-1 +2a 3-2 =a 2 +2a 1 =11+2*7=11+14=25
● From the above options ,Substitute the r values 0,1,2,3 then option -D gives the solution to recurrence relation. “
- Next Quiz Daily at navclasses.in 12 PM
- Paper 2 Sunday at navclasses.in
Study Paper 1 Topics for Free Click Here
Get subscription for Complete Preparation NTA NET JRF: https://unacademy.com/subscribe/TEWDQ
use my referral code for 10% additional discount: NAVCLASSES
Search Navdeep Kaur and start watching ongoing courses
NTA NET Paper 1
Paper 2 CS Discrete Structures and Optimization Part 4
Quiz-summary
0 of 30 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
Information
Paper 1 Quiz helps u to Excel in NET JRF
Paper 1 All questions 2 Marks each
- Navdeep Kaur
- All the Best
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Results
0 of 30 questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 points, (0)
| Average score |
|
| Your score |
|
Categories
- Not categorized 0%
-
Average marks Improve next time All the Best
-
Nice Keep it up, Stay Blessed
-
Awesome Great Marks, Keep doing
| Pos. | Name | Entered on | Points | Result |
|---|---|---|---|---|
| Table is loading | ||||
| No data available | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- Answered
- Review
-
Question 1 of 30
1. Question
2 pointsConsider a Hamiltonian Graph G with no loops or parallel edges and with |V(G)| = n ≥ 3. Then which of the following is true ?
Correct
With the help of dirac’s theorem, we can prove above three statements.
Incorrect
With the help of dirac’s theorem, we can prove above three statements.
-
Question 2 of 30
2. Question
2 points“How many multiples of 6 are there between the following pairs of numbers ?
0 and 100 and –6 and 34”Correct
“0 and 100 → Counting sequentially:
0,6,12,18,24,30,36,42,48,54,60,66,72,78,84,90,96 Total=17
–6 and 34 → Counting sequentially: -6,0,6,12,18,24,30
Total=7 “Incorrect
“0 and 100 → Counting sequentially:
0,6,12,18,24,30,36,42,48,54,60,66,72,78,84,90,96 Total=17
–6 and 34 → Counting sequentially: -6,0,6,12,18,24,30
Total=7 “ -
Question 3 of 30
3. Question
2 pointsThe functions mapping R into R are defined as : f(x) = x 3 – 4x, g(x) = 1/(x 2 + 1) and h(x) = x 4 . Then find the value of the following composite functions : hog(x) and hogof(x)
Correct
“Step-1: Given data,
f(x) = x^3 – 4x, g(x) = 1/(x^ 2 + 1) and h(x) = x ^4
hog(x)=h(1/(x ^2 + 1))
=h(1/(x ^2 )+1)^ 4
= 1/(x^ 2 +1)^ 4
= (x ^2 +1) ^-4
hogof(x)= hog(x^ 3 -4x)
= h(1/(x^ 3 -4x)^ 2 +1)
= h(1/(x^ 3 -4x)^ 2 +1)^ 4
= h((x^ 3 -4x)^ 2 +1)^ -4
So, option D id is correct answer. “Incorrect
“Step-1: Given data,
f(x) = x^3 – 4x, g(x) = 1/(x^ 2 + 1) and h(x) = x ^4
hog(x)=h(1/(x ^2 + 1))
=h(1/(x ^2 )+1)^ 4
= 1/(x^ 2 +1)^ 4
= (x ^2 +1) ^-4
hogof(x)= hog(x^ 3 -4x)
= h(1/(x^ 3 -4x)^ 2 +1)
= h(1/(x^ 3 -4x)^ 2 +1)^ 4
= h((x^ 3 -4x)^ 2 +1)^ -4
So, option D id is correct answer. “ -
Question 4 of 30
4. Question
2 points“Consider a sequence F 00 defined as : F 00 (0) = 1, F 00 (1) = 1
F 00 (n) = ((10 ∗ F 00 (n – 1) + 100)/ F 00 (n – 2)) for n ≥ 2 Then what shall be the set of values of the sequence F 00 ?”Correct
“Given data,
Sequence F 00 defined as
F 00 (0) = 1,
F 00 (1) = 1,
F 00 (n) = ((10 ∗ F 00 (n – 1) + 100)/ F 00 (n – 2)) for n ≥ 2
Let n=2
F 00 (2) = (10 * F 00 (1) + 100) / F 00 (2 – 2)
= (10 * 1 + 100) / 1
= (10 + 100) / 1
= 110
Let n=3
F 00 (3) = (10 * F 00 (2) + 100) / F 00 (3 – 2)
= (10 * 110 + 100) / 1
= (1100 + 100) / 1
= 1200
Similarly, n=4
F 00 (4) = (10 * F 00 (3) + 100) / F 00 (4 – 2)
= (12100) / 110
= 110
F 00 (5) = (10 * F 00 (4) + 100) / F 00 (5 – 2)
= (10*110 + 100) / 1200
= 1
The sequence will be (1, 110, 1200,110, 1). “Incorrect
“Given data,
Sequence F 00 defined as
F 00 (0) = 1,
F 00 (1) = 1,
F 00 (n) = ((10 ∗ F 00 (n – 1) + 100)/ F 00 (n – 2)) for n ≥ 2
Let n=2
F 00 (2) = (10 * F 00 (1) + 100) / F 00 (2 – 2)
= (10 * 1 + 100) / 1
= (10 + 100) / 1
= 110
Let n=3
F 00 (3) = (10 * F 00 (2) + 100) / F 00 (3 – 2)
= (10 * 110 + 100) / 1
= (1100 + 100) / 1
= 1200
Similarly, n=4
F 00 (4) = (10 * F 00 (3) + 100) / F 00 (4 – 2)
= (12100) / 110
= 110
F 00 (5) = (10 * F 00 (4) + 100) / F 00 (5 – 2)
= (10*110 + 100) / 1200
= 1
The sequence will be (1, 110, 1200,110, 1). “ -
Question 5 of 30
5. Question
2 pointsNegation of the proposition ∃x H(x) is:
Correct
Take negation inside.
Incorrect
Take negation inside.
-
Question 6 of 30
6. Question
2 points“Let P and Q be two propositions, ¬ (P ↔ Q) is equivalent to:
(I) P ↔ ¬ Q
(II) ¬ P ↔ Q
(III) ¬ P ↔ ¬ Q
(IV) Q → P “Correct
 Incorrect
Incorrect

-
Question 7 of 30
7. Question
2 points“How many distinguishable permutations of the letters in the word BANANA are there ?
Correct
“Total distinguishable permutations means no repetition.
BANANA= 6 letters
B is appearing 1 time
A is appearing 3 times
N is appearing 2 times
So, = 6! / (3! * 2!)
= 60 “Incorrect
“Total distinguishable permutations means no repetition.
BANANA= 6 letters
B is appearing 1 time
A is appearing 3 times
N is appearing 2 times
So, = 6! / (3! * 2!)
= 60 “ -
Question 8 of 30
8. Question
2 pointsThe sum of the series: (1/2) + (1/3) + (1/4) – (1/6) + (1/8) + (1/9) + (1/16) – (1/12) + … + α is:
Correct
The sum of the series: (1/2) + (1/3) + (1/4) – (1/6) + (1/8) + (1/9) + (1/16) – (1/12) + … + α is 1 + log(√2)3.
Incorrect
The sum of the series: (1/2) + (1/3) + (1/4) – (1/6) + (1/8) + (1/9) + (1/16) – (1/12) + … + α is 1 + log(√2)3.
-
Question 9 of 30
9. Question
2 pointsIf a lattice (L,R) has a greatest and least element then it is said to be:
Correct
“→ In a Lattice if Upper Bound and Lower exists then it is called Bounded Lattice.
→ A bounded lattice is an algebraic structure of the form (L, ∨, ∧, 0, 1) such that (L, ∨, ∧) is a lattice, 0 (the lattice’s bottom) is the identity element for the join operation ∨, and 1 (the lattice top) is the identity element for the meet operation ∧.
→ Let ‘L’ be a lattice w.r.t R if there exists an element I∈L such that (aRI)∀x∈L, then I is called Upper Bound of a Lattice L.
Similarly, if there exists an element O∈L such that (ORa)∀a∈L, then O is called Lower Bound of Lattice L. “Incorrect
“→ In a Lattice if Upper Bound and Lower exists then it is called Bounded Lattice.
→ A bounded lattice is an algebraic structure of the form (L, ∨, ∧, 0, 1) such that (L, ∨, ∧) is a lattice, 0 (the lattice’s bottom) is the identity element for the join operation ∨, and 1 (the lattice top) is the identity element for the meet operation ∧.
→ Let ‘L’ be a lattice w.r.t R if there exists an element I∈L such that (aRI)∀x∈L, then I is called Upper Bound of a Lattice L.
Similarly, if there exists an element O∈L such that (ORa)∀a∈L, then O is called Lower Bound of Lattice L. “ -
Question 10 of 30
10. Question
2 pointsIf a relation < from A={1,2,3,4} to B={1,3,5} i.e., (a,b)∈R if a < b, then R-1 is:
Correct
The relation R is {(1,3), (1,5),(2,3),(2,5),(3,5),(4,5) } where (a,b) ∈ R if a The R-1 is { (3,1),(5,1),(3,2),(5,2),(5,3),(5,4) } where (a,b) ∈ R-1 if a>b.
Incorrect
The relation R is {(1,3), (1,5),(2,3),(2,5),(3,5),(4,5) } where (a,b) ∈ R if a The R-1 is { (3,1),(5,1),(3,2),(5,2),(5,3),(5,4) } where (a,b) ∈ R-1 if a>b.
-
Question 11 of 30
11. Question
2 pointsThe number of two digit numbers divisible by the product of digits is:
Correct
“11=1*1=1 which is a factor of 11
12=1*2=2 which is a factor of 12
15=1*5=5 which is a factor of 15
24=2*4=8 which is a factor of 24
36=3*6=12 which is a factor of 36 “Incorrect
“11=1*1=1 which is a factor of 11
12=1*2=2 which is a factor of 12
15=1*5=5 which is a factor of 15
24=2*4=8 which is a factor of 24
36=3*6=12 which is a factor of 36 “ -
Question 12 of 30
12. Question
2 pointsIn algebra of logic, the conjunction of two tautologies is:
Correct
“Some properties are tautologies:
1. The negation of a contradiction is a tautology.
2. The disjunction of two contingencies can be a tautology.
3. The conjunction of two tautologies is a tautology. “Incorrect
“Some properties are tautologies:
1. The negation of a contradiction is a tautology.
2. The disjunction of two contingencies can be a tautology.
3. The conjunction of two tautologies is a tautology. “ -
Question 13 of 30
13. Question
2 pointsHow many integers are between 1 and 200 which are divisible by any one of the integers 2,3 and 5(Hint: use set operation)?
Correct
“A) numbers divisible by 2: 200/2 = 100
B) numbers divisible by 3: 200/3 = 66
C) numbers divisible by 5: 200/5 = 40
Counting twice:
AB) numbers divisible by 6: 200/6 = 33
AC) numbers divisible by 10: 200/10 = 20
BC) numbers divisible by 15: 200/15 = 13
Counting 3 times:
ABC) numbers divisible by 30: 200/30 = 6
Total of numbers = A + B + C – AB – AC – BC + ABC = 100 + 66 + 40 – 33 – 20 -13 + 6 = 146 “Incorrect
“A) numbers divisible by 2: 200/2 = 100
B) numbers divisible by 3: 200/3 = 66
C) numbers divisible by 5: 200/5 = 40
Counting twice:
AB) numbers divisible by 6: 200/6 = 33
AC) numbers divisible by 10: 200/10 = 20
BC) numbers divisible by 15: 200/15 = 13
Counting 3 times:
ABC) numbers divisible by 30: 200/30 = 6
Total of numbers = A + B + C – AB – AC – BC + ABC = 100 + 66 + 40 – 33 – 20 -13 + 6 = 146 “ -
Question 14 of 30
14. Question
2 pointsThe sum of n terms of 1/(1*2) + 1/(2*3) + 1/(3*4) + … is
Correct
“Sum upto n terms = 1/(1*2) + 1/(2*3) + 1/(3*4) + …….. + 1/(n*(n+1))
where
1st term = 1/(1*2)
2nd term = 1/(2*3)
3rd term = 1/(3*4)
.
.
.
.
n-th term = 1/(n*(n+1))
n-th term = 1/(n*(n+1))
i.e. the k-th term is of the form 1/(k*(k+1))
which can further be written as k-th term = 1/k – 1/(k+1)
So, sum upto n terms can be calculated as:
(1/1 – 1/1+1) + (1/2 – 1/2+1) + (1/3 – 1/3+1) + ……… + (1/n-1 – /1n) + (1/n – 1/n+1)
= (1 – 1/2) + (1/2 – 1/3) + (1/3 – 1/4) + ……… + (1/n-1 – 1/n) + (1/n – 1/n+1)
= 1 – 1/n+1
= ((n+1) – 1)/n+1
= n/n+1 “Incorrect
“Sum upto n terms = 1/(1*2) + 1/(2*3) + 1/(3*4) + …….. + 1/(n*(n+1))
where
1st term = 1/(1*2)
2nd term = 1/(2*3)
3rd term = 1/(3*4)
.
.
.
.
n-th term = 1/(n*(n+1))
n-th term = 1/(n*(n+1))
i.e. the k-th term is of the form 1/(k*(k+1))
which can further be written as k-th term = 1/k – 1/(k+1)
So, sum upto n terms can be calculated as:
(1/1 – 1/1+1) + (1/2 – 1/2+1) + (1/3 – 1/3+1) + ……… + (1/n-1 – /1n) + (1/n – 1/n+1)
= (1 – 1/2) + (1/2 – 1/3) + (1/3 – 1/4) + ……… + (1/n-1 – 1/n) + (1/n – 1/n+1)
= 1 – 1/n+1
= ((n+1) – 1)/n+1
= n/n+1 “ -
Question 15 of 30
15. Question
2 pointsA declarative sentence which is either true(1) or false(0) is called:
Correct
“• Declarative sentences are propositions.
• Sentences that assert a fact that could either be true or false. “Incorrect
“• Declarative sentences are propositions.
• Sentences that assert a fact that could either be true or false. “ -
Question 16 of 30
16. Question
2 pointsRank of nonsingular square matrix of order r is:
Correct
“• A square matrix of order ’r’ is nonsingular if its determinant is non zero and therefore its rank is “r”. It’s all rows and columns are linearly independent and it is invertible.
• Rank of singular matrix is less than “r”. “Incorrect
“• A square matrix of order ’r’ is nonsingular if its determinant is non zero and therefore its rank is “r”. It’s all rows and columns are linearly independent and it is invertible.
• Rank of singular matrix is less than “r”. “ -
Question 17 of 30
17. Question
2 pointsA minimal subgraph G’ of G such that V(G’)=V(G) and G’ is connected is called:
Correct
Given a connected graph G, a connected subgraph that is both a tree and contains all the vertices of G is called a spanning tree for G.Given a connected graph G, a connected subgraph that is both a tree and contains all the vertices of G is called a spanning tree for G.
Incorrect
Given a connected graph G, a connected subgraph that is both a tree and contains all the vertices of G is called a spanning tree for G.
-
Question 18 of 30
18. Question
2 pointsIf k parallel lines of a determinant Δ become identical when x=a, then ____ is a factor of Δ.
Correct
“• If a determinant D vanishes for x = a, then (x – a) is a factor of D, in other words, if two rows (or two columns) become identical for x = a, then (x-a) is a factor of D.
• In general, if k rows (or k columns) become identical (x=a) when a is substituted for x, then (x-a)r-1 is a factor of D. “Incorrect
“• If a determinant D vanishes for x = a, then (x – a) is a factor of D, in other words, if two rows (or two columns) become identical for x = a, then (x-a) is a factor of D.
• In general, if k rows (or k columns) become identical (x=a) when a is substituted for x, then (x-a)r-1 is a factor of D. “ -
Question 19 of 30
19. Question
2 pointsIn how many ways can a committee of 4 people be chosen from a group of 12?
Correct
“As the order of people does not matter, it is C4 12
C(n,r) = C(12,4)
= 12! / [(4!(12−4)!)]
= 495
Hence, a committee of 4 people be selected from a group of 12 people in 495 ways. “Incorrect
“As the order of people does not matter, it is C4 12
C(n,r) = C(12,4)
= 12! / [(4!(12−4)!)]
= 495
Hence, a committee of 4 people be selected from a group of 12 people in 495 ways. “ -
Question 20 of 30
20. Question
2 pointsHow many 3 digit numbers are there with all different odd digits?
Correct
“• Three digit odd numbers implies the numbers would only be made of digits 1 , 3 , 5 , 7 , 9 With repetition of digits we would have had 5 * 5 * 5 = 125
• But for every hundreds, maximum of 4 tens is possible (avoiding the duplicate of digit used in hundreds)
• And each of these 4 tens, maximum of 3 units is possible (avoiding the duplicate of digits used in tens)
• 5 * 4 * 3 = 60 “Incorrect
“• Three digit odd numbers implies the numbers would only be made of digits 1 , 3 , 5 , 7 , 9 With repetition of digits we would have had 5 * 5 * 5 = 125
• But for every hundreds, maximum of 4 tens is possible (avoiding the duplicate of digit used in hundreds)
• And each of these 4 tens, maximum of 3 units is possible (avoiding the duplicate of digits used in tens)
• 5 * 4 * 3 = 60 “ -
Question 21 of 30
21. Question
2 pointsThe root mean square deviation when measured from the mean is:
Correct
The root mean square deviation when measured from the mean is least value.
Incorrect
The root mean square deviation when measured from the mean is least value.
-
Question 22 of 30
22. Question
2 pointsThe mean, mode and median are connected by the empirical relationship:
Correct
 Incorrect
Incorrect

-
Question 23 of 30
23. Question
2 pointsThe algebraic sum of the deviations of all the variables from their mean is
Correct
The sum of the deviations from the mean is zero. This will always be the case as it is a property of the sample mean, i.e., the sum of the deviations below the mean will always equal the sum of the deviations above the mean. However, the goal is to capture the magnitude of these deviations in a summary measure.
Incorrect
The sum of the deviations from the mean is zero. This will always be the case as it is a property of the sample mean, i.e., the sum of the deviations below the mean will always equal the sum of the deviations above the mean. However, the goal is to capture the magnitude of these deviations in a summary measure.
-
Question 24 of 30
24. Question
2 pointsExponential distribution is special case of ____ distribution.
Correct
The exponential distribution is not the same as the class of exponential families of distributions, which is a large class of probability distributions that includes the exponential distribution as one of its members, but also includes the normal distribution, binomial distribution, gamma distribution, Poisson, and many others.
Incorrect
The exponential distribution is not the same as the class of exponential families of distributions, which is a large class of probability distributions that includes the exponential distribution as one of its members, but also includes the normal distribution, binomial distribution, gamma distribution, Poisson, and many others.
-
Question 25 of 30
25. Question
2 pointsThe normal curve is symmetrical about its:
Correct
Symmetrical distribution occurs when the values of variables occur at regular frequencies and the mean, median and mode occur at the same point. In graph form, symmetrical distribution often appears as a bell curve. If a line were drawn dissecting the middle of the graph, it would show two sides that mirror each other.
Incorrect
Symmetrical distribution occurs when the values of variables occur at regular frequencies and the mean, median and mode occur at the same point. In graph form, symmetrical distribution often appears as a bell curve. If a line were drawn dissecting the middle of the graph, it would show two sides that mirror each other.
-
Question 26 of 30
26. Question
2 pointsThe standard deviation of binomial distribution with n observations and probability of success p, probability of failure is q is:
Correct
 Incorrect
Incorrect

-
Question 27 of 30
27. Question
2 pointsIf the mean of a poisson distribution is m, then standard deviation of the distribution is:
Correct
Standard formula
Incorrect
Standard formula
-
Question 28 of 30
28. Question
2 pointsIf a random variable takes a finite set of values it is called:
Correct
“→ A discrete variable is a variable whose value is obtained by counting.
Examples:
number of students present
number of red marbles in a jar
number of heads when flipping three coins
students’ grade level
→ A discrete random variable X has a countable number of possible values.
Example:
Let X represent the sum of two dice.
→ A discrete random variable is one which may take on only a countable number of distinct values such as 0,1,2,3,4,…….. Discrete random variables are usually (but not necessarily) counts. If a random variable can take only a finite number of distinct values, then it must be discrete.
Examples of discrete random variables include the number of children in a family, the Friday night attendance at a cinema, the number of patients in a doctor’s surgery, the number of defective light bulbs in a box of ten. “Incorrect
“→ A discrete variable is a variable whose value is obtained by counting.
Examples:
number of students present
number of red marbles in a jar
number of heads when flipping three coins
students’ grade level
→ A discrete random variable X has a countable number of possible values.
Example:
Let X represent the sum of two dice.
→ A discrete random variable is one which may take on only a countable number of distinct values such as 0,1,2,3,4,…….. Discrete random variables are usually (but not necessarily) counts. If a random variable can take only a finite number of distinct values, then it must be discrete.
Examples of discrete random variables include the number of children in a family, the Friday night attendance at a cinema, the number of patients in a doctor’s surgery, the number of defective light bulbs in a box of ten. “ -
Question 29 of 30
29. Question
2 pointsM is a square matrix of order ‘n’ and its determinant value is 5. If all the elements of M are multiplied by 2, Its determinant value becomes 40. The value of ‘n’ is
Correct
“● From the matrix property : If each element of a row (or a column) of a determinant is multiplied by a constant k, then its value gets multiplied by k.
● Consider matrix order is 3, there are 3 rows and each row is multiplied by 2 means we need to multiply 8 to the existing determinant.
● The given existing determinant is 5 and each row multiplied by 2 means 8 *5 =40. “Incorrect
“● From the matrix property : If each element of a row (or a column) of a determinant is multiplied by a constant k, then its value gets multiplied by k.
● Consider matrix order is 3, there are 3 rows and each row is multiplied by 2 means we need to multiply 8 to the existing determinant.
● The given existing determinant is 5 and each row multiplied by 2 means 8 *5 =40. “ -
Question 30 of 30
30. Question
2 pointsThe solution of the recurrence relation a r =a r-1 +2a r-2 with a 0 =2,a 1 =7
Correct
“● Given the recurrence relation a r =a r-1 +2a r-2 and a 0 =2,a 1 =7.
● For r =2, a 2= a 2-1 +2a 2-2 =a 1 +2a 0 =7+2*2=7+4=11 ● For r=3,a 3= a 3-1 +2a 3-2 =a 2 +2a 1 =11+2*7=11+14=25
● From the above options ,Substitute the r values 0,1,2,3 then option -D gives the solution to recurrence relation. “Incorrect
“● Given the recurrence relation a r =a r-1 +2a r-2 and a 0 =2,a 1 =7.
● For r =2, a 2= a 2-1 +2a 2-2 =a 1 +2a 0 =7+2*2=7+4=11 ● For r=3,a 3= a 3-1 +2a 3-2 =a 2 +2a 1 =11+2*7=11+14=25
● From the above options ,Substitute the r values 0,1,2,3 then option -D gives the solution to recurrence relation. “






