- Quiz will start as soon as you click the ‘Start Quiz‘ button below.
- Question will come one by one click on next for next question
- There are 30 questions in this quiz, you will get 30 Minutes to attempt.
- 2 Marks is determined for the correct answer for each question. There is no negative marking for incorrect answer.
- After the quiz is over, in order to know your rank in the Ranking List / Leader-board below, you should enter your name and email address, otherwise you will be deprived of it.
- After completing click on finish Quiz
- To see correct answers click on view Question
- जैसे ही आप नीचे दिए गए ‘स्टार्ट क्विज़’ बटन पर क्लिक करेंगे, क्विज़ शुरू हो जाएगा।
प्रश्न अगले प्रश्न के लिए अगले एक क्लिक पर आएगा
इस क्विज में 30 प्रश्न हैं, आपको प्रयास करने के लिए 30 मिनट मिलेंगे।
प्रत्येक प्रश्न के सही उत्तर के लिए 2 अंक निर्धारित किए गए हैं। गलत उत्तर के लिए कोई नकारात्मक अंकन नहीं है।
प्रश्नोत्तरी समाप्त होने के बाद, नीचे दी गई रैंकिंग सूची / लीडर-बोर्ड में अपनी रैंक जानने के लिए, आपको अपना नाम और ईमेल पता दर्ज करना चाहिए, अन्यथा आप इससे वंचित रह जाएंगे।
फिनिश क्विज़ पर क्लिक करने के बाद
सही उत्तर देखने के लिए प्रश्न पर क्लिक करें
Paper 2 CS Discrete Structures and Optimization Part 2
Quiz-summary
0 of 30 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
Information
Paper 1 Quiz helps u to Excel in NET JRF
Paper 1 All questions 2 Marks each
- Navdeep Kaur
- All the Best
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Results
0 of 30 questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 points, (0)
| Average score |
|
| Your score |
|
Categories
- Not categorized 0%
-
Average marks Improve next time All the Best
-
Nice Keep it up, Stay Blessed
-
Awesome Great Marks, Keep doing
| Pos. | Name | Entered on | Points | Result |
|---|---|---|---|---|
| Table is loading | ||||
| No data available | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- Answered
- Review
-
Question 1 of 30
1. Question
2 pointsAn undirected graph possesses an eulerian circuit if and only if it is connected and its vertices are एक अप्रत्यक्ष ग्राफ में एक यूलरियन सर्किट होता है, यदि और केवल यदि यह जुड़ा हुआ है और इसके कोने हैं
Correct
“→ An undirected graph possesses an eulerian circuit if and only if it is connected and its vertices all of even degree.
→ Eulerian circuit (or) Euler tour in an undirected graph is a cycle that uses each edge exactly once. “Incorrect
“→ An undirected graph possesses an eulerian circuit if and only if it is connected and its vertices all of even degree.
→ Eulerian circuit (or) Euler tour in an undirected graph is a cycle that uses each edge exactly once. “ -
Question 2 of 30
2. Question
2 pointsThe number of integers between 1 and 250 that are divisible by 2, 5 and 7 is 1 और 250 के बीच पूर्णांकों की संख्या जो 2, 5 और 7 से विभाज्य है
Correct
“Here, we have to find all possible integers between 250 which was divisible by 2,5 and 7.
Solving this problem by 2 methods:
1. Venn diagram
2. Mathematical substitution.
In this problem, we are using Mathematical substitution method.
Step-1: According to condition, we can perform least common multiple(LCM) of 2,5 and 7=70
Step-2: Total number of integers= ⌊250/70⌋
= 3
Note: Divisible numbers are 70,140 and 210. “Incorrect
“Here, we have to find all possible integers between 250 which was divisible by 2,5 and 7.
Solving this problem by 2 methods:
1. Venn diagram
2. Mathematical substitution.
In this problem, we are using Mathematical substitution method.
Step-1: According to condition, we can perform least common multiple(LCM) of 2,5 and 7=70
Step-2: Total number of integers= ⌊250/70⌋
= 3
Note: Divisible numbers are 70,140 and 210. “ -
Question 3 of 30
3. Question
2 pointsIn a multi-user operating system, 20 requests are made to use a particular resource per hour, on an average. The probability that no requests are made in 45 minutes is एक बहु-उपयोगकर्ता ऑपरेटिंग सिस्टम में, औसतन प्रति घंटे एक विशेष संसाधन का उपयोग करने के लिए 20 अनुरोध किए जाते हैं। संभावना है कि 45 मिनट में कोई अनुरोध नहीं किया जाता है
Correct
“Probability of events for a Poisson distribution:
An event can occur 0, 1, 2, … times in an interval. The average number of events in an interval is designated (lambda). is the event rate, also called the rate parameter. The probability of observing k events in an interval is given by the equation
P(k events in interval)=e-λ [(λk)/k!]
Where
→ λ is the average number of events per interval
→ e is the number 2.71828… (Euler’s number) the base of the natural logarithms
→ k takes values 0, 1, 2, …
→ k! = k × (k − 1) × (k − 2) × … × 2 × 1 is the factorial of k.
→ Now it is given that in 1 hour (60 minutes) 20 requests are made
→ In 1 minute number of requests made= 20/60
→ In 45 minutes total number of requests made = (20/60) * 45
= 15
Probability= (e-15 *(15)0) / 0!
= e-15 “Incorrect
“Probability of events for a Poisson distribution:
An event can occur 0, 1, 2, … times in an interval. The average number of events in an interval is designated (lambda). is the event rate, also called the rate parameter. The probability of observing k events in an interval is given by the equation
P(k events in interval)=e-λ [(λk)/k!]
Where
→ λ is the average number of events per interval
→ e is the number 2.71828… (Euler’s number) the base of the natural logarithms
→ k takes values 0, 1, 2, …
→ k! = k × (k − 1) × (k − 2) × … × 2 × 1 is the factorial of k.
→ Now it is given that in 1 hour (60 minutes) 20 requests are made
→ In 1 minute number of requests made= 20/60
→ In 45 minutes total number of requests made = (20/60) * 45
= 15
Probability= (e-15 *(15)0) / 0!
= e-15 “ -
Question 4 of 30
4. Question
2 pointsThe truth value of the statements : ∃!xP(x) → ∃xP(x) and ∃!x ⌐P(x) →⌐∀xP(x), (where the notation ∃!xP(x) denotes the proposition “There exists a unique x such that P(x) is true”) are : बयानों का सत्य मूल्य: ∃! XP (x) → (xP (x) और ∃! X )P (x) → PxP (x), (जहां संकेतन x! XP (x) प्रस्ताव को दर्शाता है) एक विशिष्ट x मौजूद है जैसे P (x) सत्य है)
Correct
“From the given question, → The symbol ∃ is call the existential quantifier and represents the phrase “there exists” or “for some”. The existential quantification of P(x) is the statement “P(x) for some values x in the universe”, or equivalently, “There exists a value for x such that P(x) is true”, which is written ∃xP(x). So the statement ∃!xP(x) → ∃xP(x) is true.
→ If P(x) is true for at least one element in the domain, then ∃xP(x) is true. Otherwise it is false.
→ Accordingly DeMorgan’s laws for quantifiers:the following statements are true.
¬∀xP(x) ≡ ∃x¬P(x)
¬∃xP(x) ≡ ∀x¬P(x) then the statement is ∃!x ⌐P(x) →⌐∀xP(x) is true. “Incorrect
“From the given question, → The symbol ∃ is call the existential quantifier and represents the phrase “there exists” or “for some”. The existential quantification of P(x) is the statement “P(x) for some values x in the universe”, or equivalently, “There exists a value for x such that P(x) is true”, which is written ∃xP(x). So the statement ∃!xP(x) → ∃xP(x) is true.
→ If P(x) is true for at least one element in the domain, then ∃xP(x) is true. Otherwise it is false.
→ Accordingly DeMorgan’s laws for quantifiers:the following statements are true.
¬∀xP(x) ≡ ∃x¬P(x)
¬∃xP(x) ≡ ∀x¬P(x) then the statement is ∃!x ⌐P(x) →⌐∀xP(x) is true. “ -
Question 5 of 30
5. Question
2 pointsWhich of the following shall be a compound proposition involving the propositions p, q and r, that is true when exactly two of the p, q and r are true and is false otherwise निम्नलिखित में से कौन सा एक प्रस्ताव प्रस्ताव होगा जिसमें प्रस्ताव p, q और r शामिल होगा, यह तब सच है जब p, q और r में से दो सही हों और अन्यथा गलत हों
Correct
“From the question, the propositions consists of exactly two of the variables should true and final proposition should be true.
Only option C consists of exactly two of the variables are true and all remaining variables deviating this rule.
In this proposition, (p ∧ q ∧⌐ r) ∨ ( p ∧ ⌐q ∧ r) ∨ (⌐ p ∧ q ∧ r)
(p ∧ q ∧⌐ r) → p and q are true
( p ∧ ⌐q ∧ r) → p and r are true
(⌐ p ∧ q ∧ r) → q and r are true
Finally the proposition consists of “V” operation , so the entire proposition is true. “Incorrect
“From the question, the propositions consists of exactly two of the variables should true and final proposition should be true.
Only option C consists of exactly two of the variables are true and all remaining variables deviating this rule.
In this proposition, (p ∧ q ∧⌐ r) ∨ ( p ∧ ⌐q ∧ r) ∨ (⌐ p ∧ q ∧ r)
(p ∧ q ∧⌐ r) → p and q are true
( p ∧ ⌐q ∧ r) → p and r are true
(⌐ p ∧ q ∧ r) → q and r are true
Finally the proposition consists of “V” operation , so the entire proposition is true. “ -
Question 6 of 30
6. Question
2 pointsHow many edges must be removed to produce the spanning forest of a graph with N vertices, M edges and C connected components ? एन कोने, एम किनारों और सी जुड़े घटकों के साथ ग्राफ के फैले जंगल का उत्पादन करने के लिए कितने किनारों को हटाया जाना चाहिए?
Correct
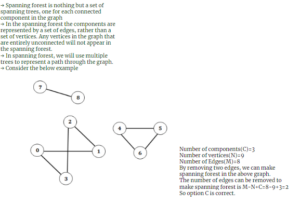 Incorrect
Incorrect

-
Question 7 of 30
7. Question
2 pointsA test contains 100 true/false questions. How many different ways can a student answer the questions on the test, if the answer may be left blank also. एक परीक्षण में 100 सच्चे / झूठे प्रश्न होते हैं। विद्यार्थी परीक्षा में प्रश्नों के कितने अलग-अलग तरीके से उत्तर दे सकता है, यदि उत्तर को खाली भी छोड़ा जा सकता है।
Correct
 Incorrect
Incorrect

-
Question 8 of 30
8. Question
2 pointsThe relation “divides” on a set of positive integers is ________. सकारात्मक पूर्णांक के एक सेट पर “विभाजन” संबंध ________ है।
Correct
“The relation “divides” on a set of positive integers is Anti symmetric and Transitive.
Proof:
Let assume a,b two set elements.
The relation is antisymmetric if and only if for every a,b in the set.
IF(a∣b AND b∣a), then it must follow that a=b.
→ If it’s FALSE then both a∣b AND b∣a, then it’s perfectly consistent to have a≠b.
→ The only time a∣b AND b∣a is exactly when a=b, since then we have a∣b ⟺ a∣a is TRUE for all a.
Hence the relation is antisymmetric. “Incorrect
“The relation “divides” on a set of positive integers is Anti symmetric and Transitive.
Proof:
Let assume a,b two set elements.
The relation is antisymmetric if and only if for every a,b in the set.
IF(a∣b AND b∣a), then it must follow that a=b.
→ If it’s FALSE then both a∣b AND b∣a, then it’s perfectly consistent to have a≠b.
→ The only time a∣b AND b∣a is exactly when a=b, since then we have a∣b ⟺ a∣a is TRUE for all a.
Hence the relation is antisymmetric. “ -
Question 9 of 30
9. Question
2 points“Cyclometric complexity of a flow graph G with n vertices and e edges is
“”एन कोने और ई किनारों के साथ एक प्रवाह ग्राफ जी का साइक्लोमैटिक जटिलता है”Correct
“Cyclomatic complexity uses 3 formulas:
1. The number of regions corresponds to the cyclomatic complexity
2. V(G),Flow graph is defined as V(G)=E-N+2 where E is the number of flow graph edges, and N is the number of flow graph nodes.
3. V(G),Flow graph is defined as V(G)=P+1 where p is the number of predicate nodes contained in the flow graph G. “Incorrect
“Cyclomatic complexity uses 3 formulas:
1. The number of regions corresponds to the cyclomatic complexity
2. V(G),Flow graph is defined as V(G)=E-N+2 where E is the number of flow graph edges, and N is the number of flow graph nodes.
3. V(G),Flow graph is defined as V(G)=P+1 where p is the number of predicate nodes contained in the flow graph G. “ -
Question 10 of 30
10. Question
2 points“The proposition ~p ∨ q is equivalent to
प्रस्ताव ~ p is q के बराबर है”Correct
Draw the truth table and A is the answer. Its a very simple question.
Incorrect
Draw the truth table and A is the answer. Its a very simple question.
-
Question 11 of 30
11. Question
2 points“Any integer composed of 3n identical digits divisible by
3n समरूप अंकों से बना कोई भी पूर्णांक विभाज्य है”Correct
“Identical digits means similar(same) digits.
Any integer composed of 3n identical digits.
For example n=1, 3n= 31=3 which means three identical digits (111,222,333,444 and so on)
n=2, 32 =9 which means nine identical digits (111111111, 222222222 and so on)
The above numbers are is divisible by 3
111 is divisible by 3.
222, 333 and 444 are multiple of 3 “Incorrect
“Identical digits means similar(same) digits.
Any integer composed of 3n identical digits.
For example n=1, 3n= 31=3 which means three identical digits (111,222,333,444 and so on)
n=2, 32 =9 which means nine identical digits (111111111, 222222222 and so on)
The above numbers are is divisible by 3
111 is divisible by 3.
222, 333 and 444 are multiple of 3 “ -
Question 12 of 30
12. Question
2 pointsWhat is the probability of choosing correctly an unknown integer between 0 and 9 with 3 chances ? 3 अवसरों के साथ 0 और 9 के बीच एक अज्ञात पूर्णांक को सही ढंग से चुनने की संभावना क्या है?
Correct
“Probability of getting a number = 1/10
Probability of not getting a number = 1- 1/(10) = 9/10
Now probability that correct number is chosen in first chance= 1/10
probability that correct number is chosen in second chance= (9/10)* (1/10)
probability that correct number is chosen in first chance= (9/10)* (9/10) *(1/10)
So total probability = (1/10)+ [(9/10)* (1/10) ]+ [(9/10)* (9/10) *(1/10)]
= (1/10)+(9/100)+(81/1000)
= 271/1000, Hence none of the above “Incorrect
“Probability of getting a number = 1/10
Probability of not getting a number = 1- 1/(10) = 9/10
Now probability that correct number is chosen in first chance= 1/10
probability that correct number is chosen in second chance= (9/10)* (1/10)
probability that correct number is chosen in first chance= (9/10)* (9/10) *(1/10)
So total probability = (1/10)+ [(9/10)* (1/10) ]+ [(9/10)* (9/10) *(1/10)]
= (1/10)+(9/100)+(81/1000)
= 271/1000, Hence none of the above “ -
Question 13 of 30
13. Question
2 pointsThe proposition ~qvp is equivalent to प्रस्ताव ~ qvp के बराबर है
Correct
Draw the truth table
Incorrect
Draw the truth table
-
Question 14 of 30
14. Question
2 pointsA hash table has space for 75 records, then the probability of collision before the table is 6% full. एक हैश तालिका में 75 रिकॉर्ड के लिए जगह है, फिर तालिका से पहले टकराव की संभावना 6% भरी हुई है।
Correct
“Given data,
— Hash table has space =75 slots.
— For 6% filling it must take =6 slots.
— Probability of no collision for first 6 entries=?
Step-1: According to given data,
= (75P6) / (756)
= 0.814586387
Step-2: We have to find at least one collision occurs in 6 entries
=1-Probability of no collision for first 6 entries
= 1-0.814586387
= 0.185413613 , Hence none of the above “Incorrect
“Given data,
— Hash table has space =75 slots.
— For 6% filling it must take =6 slots.
— Probability of no collision for first 6 entries=?
Step-1: According to given data,
= (75P6) / (756)
= 0.814586387
Step-2: We have to find at least one collision occurs in 6 entries
=1-Probability of no collision for first 6 entries
= 1-0.814586387
= 0.185413613 , Hence none of the above “ -
Question 15 of 30
15. Question
2 pointsMaximum number of edges in a n-Node undirected graph without self loop is स्व-लूप के बिना एन-नोड अप्रत्यक्ष ग्राफ में किनारों की अधिकतम संख्या है
Correct
The set of vertices has size n, the number of such subsets is given by the binomial coefficient C(n,2)⋅C(n,2) = n(n-1)/2
Incorrect
The set of vertices has size n, the number of such subsets is given by the binomial coefficient C(n,2)⋅C(n,2) = n(n-1)/2
-
Question 16 of 30
16. Question
2 pointsThe number of colours required to properly colour the vertices of every planar graph is हर प्लानर ग्राफ के कोने को ठीक से रंगने के लिए आवश्यक रंगों की संख्या है
Correct
“→ The 4-colour theorem of the planar graph describes that any planar can at most be colored with 4 colors.
→ The sufficient number of colors in worst case is 4 colors for any planar graph. “Incorrect
“→ The 4-colour theorem of the planar graph describes that any planar can at most be colored with 4 colors.
→ The sufficient number of colors in worst case is 4 colors for any planar graph. “ -
Question 17 of 30
17. Question
2 pointsWhich of the following is an equivalence relation on the set of all functions from Z to Z ?
Correct
“An equivalence relation is a binary relation that is reflexive, symmetric and transitive.
The relation “”is equal to”” is the canonical example of an equivalence relation, where for any objects a, b, and c:
a = a (reflexive property),
if a = b then b = a (symmetric property), and
if a = b and b = c then a = c (transitive property)
“Incorrect
“An equivalence relation is a binary relation that is reflexive, symmetric and transitive.
The relation “”is equal to”” is the canonical example of an equivalence relation, where for any objects a, b, and c:
a = a (reflexive property),
if a = b then b = a (symmetric property), and
if a = b and b = c then a = c (transitive property)
“ -
Question 18 of 30
18. Question
2 pointsWhich of the relations on {0, 1, 2, 3} is an equivalence relation ?
Correct
“→ A relation on a set A is called an equivalence relation if it is reflexive, symmetric, and transitive.
1. Reflexivity: f(x) = f(x)
True, as given the same input, a function always produces the same output
2. Symmetry: if f(x) = f(y) then f(y) = f(x)
True, by the definition of equality
3.Transitivity: if f(x) = f(y) and f(y) = f(z) then f(x) = f(z)
True, by the definition of equality
Option-2: { (0,0), (1,1), (2,2), (3,3) }
Has all the properties, thus, is an equivalence relation
Option-1: { (0,0), (0,2), (2,0), (2,2), (2,3), (3,2), (3,3) }
Not reflexive: (1,1) is missing
Not transitive: (0,2) and (2,3) are in the relation, but not (0,3)
Option-3: { (0,0), (0,1) (0,2), (1,0), (1,1), (1,2), (2,0), (2,2), (3,3) }
Not symmetric: (1,2) is present, but not (2,1)
Not transitive: (2,0) and (0,1) are in the relation, but not (2,1)
Option-4: Similarly, option-4 also not TRUE “Incorrect
“→ A relation on a set A is called an equivalence relation if it is reflexive, symmetric, and transitive.
1. Reflexivity: f(x) = f(x)
True, as given the same input, a function always produces the same output
2. Symmetry: if f(x) = f(y) then f(y) = f(x)
True, by the definition of equality
3.Transitivity: if f(x) = f(y) and f(y) = f(z) then f(x) = f(z)
True, by the definition of equality
Option-2: { (0,0), (1,1), (2,2), (3,3) }
Has all the properties, thus, is an equivalence relation
Option-1: { (0,0), (0,2), (2,0), (2,2), (2,3), (3,2), (3,3) }
Not reflexive: (1,1) is missing
Not transitive: (0,2) and (2,3) are in the relation, but not (0,3)
Option-3: { (0,0), (0,1) (0,2), (1,0), (1,1), (1,2), (2,0), (2,2), (3,3) }
Not symmetric: (1,2) is present, but not (2,1)
Not transitive: (2,0) and (0,1) are in the relation, but not (2,1)
Option-4: Similarly, option-4 also not TRUE “ -
Question 19 of 30
19. Question
2 points Correct
Correct
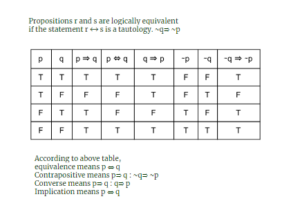 Incorrect
Incorrect

-
Question 20 of 30
20. Question
2 points“Consider the vocabulary with only four propositions A,B,C and D. How many models are there for the following sentence?
( ⌐ A ∨ ⌐ B ∨ ⌐ C ∨ ⌐ D) “”केवल चार प्रस्तावों ए, बी, सी और डी के साथ शब्दावली पर विचार करें। निम्नलिखित वाक्य में कितने मॉडल हैं?
(⌐ ए ⌐ ⌐ बी ∨ ∨ सी ⌐ “”डी)”””Correct
Here, number of models is nothing but number of TRUEs in final statement. Draw the truth table and count the “True” values in final output
Incorrect
Here, number of models is nothing but number of TRUEs in final statement. Draw the truth table and count the “True” values in final output
-
Question 21 of 30
21. Question
2 pointsIf we define the functions f, g and h that map R into R by : f(x) = x 4 , g(x) = √ x 2 + 1 , h(x) = x 2 + 72, then the value of the composite functions ho(gof) and (hog)of are given as अगर हम फ़ंक्शन को g, h और उस मैप R से R में परिभाषित करते हैं: f (x) = x 4, g (x) =) x 2 + 1, h (x) = x 2 + 72, तब समग्र कार्यों का मान हो (gof) और (हॉग) के रूप में दिया जाता है
Correct
“Given f(x) = x 4 , g(x) = √ x 2 + 1 , h(x) = x 2 + 72
for, ho(gof)
gof=g(f(x))
=g(x 4 )
=√(x 8 +1)
ho(gof)=h(gof)
=h(√(x 8 +1))
=(√(x 8 +1) 2 +72
=x 8 +1+72
=x 8 +73
√ x 2 + 1 , h(x) = x 2 + 72
for, (hog)of,
hog=h(g(x))
=h(√(x 2 +1)
=(√(x 2 +1) 2 +72
=x 2 + 1+72
=x 2 +73
(hog)of=(hog)(f(x))
=(hog)(x 4 )
=(x 4 ) 2 +73
=x 8 +73Incorrect
“Given f(x) = x 4 , g(x) = √ x 2 + 1 , h(x) = x 2 + 72
for, ho(gof)
gof=g(f(x))
=g(x 4 )
=√(x 8 +1)
ho(gof)=h(gof)
=h(√(x 8 +1))
=(√(x 8 +1) 2 +72
=x 8 +1+72
=x 8 +73
√ x 2 + 1 , h(x) = x 2 + 72
for, (hog)of,
hog=h(g(x))
=h(√(x 2 +1)
=(√(x 2 +1) 2 +72
=x 2 + 1+72
=x 2 +73
(hog)of=(hog)(f(x))
=(hog)(x 4 )
=(x 4 ) 2 +73
=x 8 +73 -
Question 22 of 30
22. Question
2 pointsA computer program selects an integer in the set {k : 1 ≤ k ≤ 10,00,000} at random and prints out the result. This process is repeated 1 million times. What is the probability that the value k=1 appears in the printout at least once ? कंप्यूटर प्रोग्राम सेट में एक पूर्णांक का चयन करता है {k: 1 ≤ k 00,000 10,00,000} यादृच्छिक पर और परिणाम को प्रिंट करता है। इस प्रक्रिया को 1 मिलियन बार दोहराया जाता है। क्या संभावना है कि मूल्य k = 1 प्रिंटआउट में कम से कम एक बार दिखाई देता है?
Correct
“Probability that the value k=1 appears in the printout at least once is
1-p(x=0)
We will apply the formula of binomial distribution
1-( 1000000 C 0 (1/1000000) 0 * (999999/1000000) 10^6 )
=1-(1*1*0.367879)
=0.632121 “Incorrect
“Probability that the value k=1 appears in the printout at least once is
1-p(x=0)
We will apply the formula of binomial distribution
1-( 1000000 C 0 (1/1000000) 0 * (999999/1000000) 10^6 )
=1-(1*1*0.367879)
=0.632121 “ -
Question 23 of 30
23. Question
2 points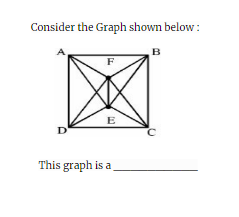 Correct
Correct
“Option-A: It is not complete graph because it won’t have n(n-1)/2 edges.
Option-B: It is not Bipartite Graph because it takes more than 2 colours. Bipartite Graph have exactly 2 colours.
Option-C: Hamiltonian path is a path in an undirected or directed graph that visits each vertex exactly once. “Incorrect
“Option-A: It is not complete graph because it won’t have n(n-1)/2 edges.
Option-B: It is not Bipartite Graph because it takes more than 2 colours. Bipartite Graph have exactly 2 colours.
Option-C: Hamiltonian path is a path in an undirected or directed graph that visits each vertex exactly once. “ -
Question 24 of 30
24. Question
2 pointsA certain tree has two vertices of degree 4, one vertex of degree 3 and one vertex of degree 2. If the other vertices have degree 1, how many vertices are there in the graph ? एक निश्चित पेड़ में डिग्री 4 के दो वर्टीकल होते हैं, डिग्री 3 के एक वर्टेक्स और डिग्री के एक वर्टेक्स 2. यदि दूसरे कोने में डिग्री 1 है, तो ग्राफ में कितने वर्टिक्स हैं?
Correct
“Here, they are clearly mentioned that “certain tree”
The tree contain maximum n-1 edges. Here, ‘n’ is number of vertices.
→ According to the handshaking lemma “sum of degrees of all vertices=2|e|”.
→ Two vertices of degree 4, we can write into (2*4)
→ One vertex of degree 3, we can write into (1*3)
→ One vertex of degree 2, we can write into (1*2).
→ Other vertices(X) have degree 1, we can write into (X*1)
Step-1: (2*4)+(1*3)+(1*2)+(X*1)
=2(X+4-1) [Note: ‘X’ value is not given ]
X=7
Step-2: To find total number of vertices, we are adding X+4 because they already given 4 vertices.
=X+4
=7+4
=11 “Incorrect
“Here, they are clearly mentioned that “certain tree”
The tree contain maximum n-1 edges. Here, ‘n’ is number of vertices.
→ According to the handshaking lemma “sum of degrees of all vertices=2|e|”.
→ Two vertices of degree 4, we can write into (2*4)
→ One vertex of degree 3, we can write into (1*3)
→ One vertex of degree 2, we can write into (1*2).
→ Other vertices(X) have degree 1, we can write into (X*1)
Step-1: (2*4)+(1*3)+(1*2)+(X*1)
=2(X+4-1) [Note: ‘X’ value is not given ]
X=7
Step-2: To find total number of vertices, we are adding X+4 because they already given 4 vertices.
=X+4
=7+4
=11 “ -
Question 25 of 30
25. Question
2 pointsConsider a set A = {1, 2, 3, …….., 1000}. How many members of A shall be divisible by 3 or by 5 or by both 3 and 5 ?
Correct
“The above problem is in the form of (AUB) = (A)+(B)-(A∩B)
A=1000/3
B=1000/5
(A∩B)=66
(AUB)=467 “Incorrect
“The above problem is in the form of (AUB) = (A)+(B)-(A∩B)
A=1000/3
B=1000/5
(A∩B)=66
(AUB)=467 “ -
Question 26 of 30
26. Question
2 pointsLet A={ x | -1 < x < 1 }=B. The function f(x)=x/2 from A to B is : A = {x | -1
Correct
“→ A function f : X → Y is defined to be one-one (or injective), if the images of distinct elements of X under f are distinct, i.e., x1 , x2 ∈ X, f(x1) = f(x2) ⇒ x1=x2.
→ The possible value of “x” is 0 then
f(x1)=x1/2=0/2=0
f(x2)=x2/2=0/2=0
for x1 , x2 ∈ X, f(x1) = f(x2) ⇒ x1 = x2. “Incorrect
“→ A function f : X → Y is defined to be one-one (or injective), if the images of distinct elements of X under f are distinct, i.e., x1 , x2 ∈ X, f(x1) = f(x2) ⇒ x1=x2.
→ The possible value of “x” is 0 then
f(x1)=x1/2=0/2=0
f(x2)=x2/2=0/2=0
for x1 , x2 ∈ X, f(x1) = f(x2) ⇒ x1 = x2. “ -
Question 27 of 30
27. Question
2 pointsFor a complete graph with N vertices, the total number of spanning trees is given by :
Correct
If a graph is complete, total number of spanning trees are N N-2
Incorrect
If a graph is complete, total number of spanning trees are N N-2
-
Question 28 of 30
28. Question
2 pointsIf (a^2 −b^2 ) is a prime number where a and b ε N, then : यदि (^ 2 −b ^ 2) एक अभाज्य संख्या है जहाँ a और b then N है, तो:
Correct
“→ For any given numbers a and b which belongs to natural numbers , the options (A) and (D) are false
→ The set of natural numbers, denoted N, can be defined in the following ways: N = {0, 1, 2, 3, …}
→ A prime number (or a prime) is a natural number greater than 1 that cannot be formed by multiplying two smaller natural numbers.
→ ‘a-b’ may be gives the non negative values which is not prime number but the a+b may give the prime value. “Incorrect
“→ For any given numbers a and b which belongs to natural numbers , the options (A) and (D) are false
→ The set of natural numbers, denoted N, can be defined in the following ways: N = {0, 1, 2, 3, …}
→ A prime number (or a prime) is a natural number greater than 1 that cannot be formed by multiplying two smaller natural numbers.
→ ‘a-b’ may be gives the non negative values which is not prime number but the a+b may give the prime value. “ -
Question 29 of 30
29. Question
2 pointsMinimum number of individual shoes to be picked up from a dark room ( containing 10 pair of shoes) if we have to get at least one proper pair :
Correct
“→ There are 10 pair of shoes available in the dark room which means 20 individual shoes are available in the room.
→ If you pick shoes from one to ten individual shoes, there may be chance of getting same individual shoes.
→ There is no guarantee that getting one proper pair from 10 individual shoes.
→ If You pick 11 shoes, then there may chance of 10 individual shoes of same type and one individual shoe of another type. So we will get at least one proper pair shoe from 11 individual shoes. “Incorrect
“→ There are 10 pair of shoes available in the dark room which means 20 individual shoes are available in the room.
→ If you pick shoes from one to ten individual shoes, there may be chance of getting same individual shoes.
→ There is no guarantee that getting one proper pair from 10 individual shoes.
→ If You pick 11 shoes, then there may chance of 10 individual shoes of same type and one individual shoe of another type. So we will get at least one proper pair shoe from 11 individual shoes. “ -
Question 30 of 30
30. Question
2 pointsConsider the relation on the set of non-negative integers defined by x ≡ y if and only if यदि और केवल यदि x and y द्वारा परिभाषित गैर-नकारात्मक पूर्णांकों के सेट पर संबंध पर विचार करें
Correct
“A relation R is an equivalence relation if and only if it is reflexive, symmetric, and transitive.
1. The relation is reflexive: x mod 3 = x mod 3
2. The relation is symmetric: if x mod 3 = y mod 3, then y mod 3 = x mod 3
3. The relation is transitive: if x mod 3 = y mod 3, and y mod 3 = z mod 3, then x mod 3 = z mod 3 “Incorrect
“A relation R is an equivalence relation if and only if it is reflexive, symmetric, and transitive.
1. The relation is reflexive: x mod 3 = x mod 3
2. The relation is symmetric: if x mod 3 = y mod 3, then y mod 3 = x mod 3
3. The relation is transitive: if x mod 3 = y mod 3, and y mod 3 = z mod 3, then x mod 3 = z mod 3 “
- Next Quiz Daily at navclasses.in 12 PM
- Paper 2 Sunday at navclasses.in
Study Paper 1 Topics for Free Click Here
Get subscription for Complete Preparation NTA NET JRF: https://unacademy.com/subscribe/TEWDQ
use my referral code for 10% additional discount: NAVCLASSES
Search Navdeep Kaur and start watching ongoing courses
NTA NET Paper 1
Paper 2 CS Discrete Structures and Optimization Part 2
Quiz-summary
0 of 30 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
Information
Paper 1 Quiz helps u to Excel in NET JRF
Paper 1 All questions 2 Marks each
- Navdeep Kaur
- All the Best
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Results
0 of 30 questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 points, (0)
| Average score |
|
| Your score |
|
Categories
- Not categorized 0%
-
Average marks Improve next time All the Best
-
Nice Keep it up, Stay Blessed
-
Awesome Great Marks, Keep doing
| Pos. | Name | Entered on | Points | Result |
|---|---|---|---|---|
| Table is loading | ||||
| No data available | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- Answered
- Review
-
Question 1 of 30
1. Question
2 pointsAn undirected graph possesses an eulerian circuit if and only if it is connected and its vertices are एक अप्रत्यक्ष ग्राफ में एक यूलरियन सर्किट होता है, यदि और केवल यदि यह जुड़ा हुआ है और इसके कोने हैं
Correct
“→ An undirected graph possesses an eulerian circuit if and only if it is connected and its vertices all of even degree.
→ Eulerian circuit (or) Euler tour in an undirected graph is a cycle that uses each edge exactly once. “Incorrect
“→ An undirected graph possesses an eulerian circuit if and only if it is connected and its vertices all of even degree.
→ Eulerian circuit (or) Euler tour in an undirected graph is a cycle that uses each edge exactly once. “ -
Question 2 of 30
2. Question
2 pointsThe number of integers between 1 and 250 that are divisible by 2, 5 and 7 is 1 और 250 के बीच पूर्णांकों की संख्या जो 2, 5 और 7 से विभाज्य है
Correct
“Here, we have to find all possible integers between 250 which was divisible by 2,5 and 7.
Solving this problem by 2 methods:
1. Venn diagram
2. Mathematical substitution.
In this problem, we are using Mathematical substitution method.
Step-1: According to condition, we can perform least common multiple(LCM) of 2,5 and 7=70
Step-2: Total number of integers= ⌊250/70⌋
= 3
Note: Divisible numbers are 70,140 and 210. “Incorrect
“Here, we have to find all possible integers between 250 which was divisible by 2,5 and 7.
Solving this problem by 2 methods:
1. Venn diagram
2. Mathematical substitution.
In this problem, we are using Mathematical substitution method.
Step-1: According to condition, we can perform least common multiple(LCM) of 2,5 and 7=70
Step-2: Total number of integers= ⌊250/70⌋
= 3
Note: Divisible numbers are 70,140 and 210. “ -
Question 3 of 30
3. Question
2 pointsIn a multi-user operating system, 20 requests are made to use a particular resource per hour, on an average. The probability that no requests are made in 45 minutes is एक बहु-उपयोगकर्ता ऑपरेटिंग सिस्टम में, औसतन प्रति घंटे एक विशेष संसाधन का उपयोग करने के लिए 20 अनुरोध किए जाते हैं। संभावना है कि 45 मिनट में कोई अनुरोध नहीं किया जाता है
Correct
“Probability of events for a Poisson distribution:
An event can occur 0, 1, 2, … times in an interval. The average number of events in an interval is designated (lambda). is the event rate, also called the rate parameter. The probability of observing k events in an interval is given by the equation
P(k events in interval)=e-λ [(λk)/k!]
Where
→ λ is the average number of events per interval
→ e is the number 2.71828… (Euler’s number) the base of the natural logarithms
→ k takes values 0, 1, 2, …
→ k! = k × (k − 1) × (k − 2) × … × 2 × 1 is the factorial of k.
→ Now it is given that in 1 hour (60 minutes) 20 requests are made
→ In 1 minute number of requests made= 20/60
→ In 45 minutes total number of requests made = (20/60) * 45
= 15
Probability= (e-15 *(15)0) / 0!
= e-15 “Incorrect
“Probability of events for a Poisson distribution:
An event can occur 0, 1, 2, … times in an interval. The average number of events in an interval is designated (lambda). is the event rate, also called the rate parameter. The probability of observing k events in an interval is given by the equation
P(k events in interval)=e-λ [(λk)/k!]
Where
→ λ is the average number of events per interval
→ e is the number 2.71828… (Euler’s number) the base of the natural logarithms
→ k takes values 0, 1, 2, …
→ k! = k × (k − 1) × (k − 2) × … × 2 × 1 is the factorial of k.
→ Now it is given that in 1 hour (60 minutes) 20 requests are made
→ In 1 minute number of requests made= 20/60
→ In 45 minutes total number of requests made = (20/60) * 45
= 15
Probability= (e-15 *(15)0) / 0!
= e-15 “ -
Question 4 of 30
4. Question
2 pointsThe truth value of the statements : ∃!xP(x) → ∃xP(x) and ∃!x ⌐P(x) →⌐∀xP(x), (where the notation ∃!xP(x) denotes the proposition “There exists a unique x such that P(x) is true”) are : बयानों का सत्य मूल्य: ∃! XP (x) → (xP (x) और ∃! X )P (x) → PxP (x), (जहां संकेतन x! XP (x) प्रस्ताव को दर्शाता है) एक विशिष्ट x मौजूद है जैसे P (x) सत्य है)
Correct
“From the given question, → The symbol ∃ is call the existential quantifier and represents the phrase “there exists” or “for some”. The existential quantification of P(x) is the statement “P(x) for some values x in the universe”, or equivalently, “There exists a value for x such that P(x) is true”, which is written ∃xP(x). So the statement ∃!xP(x) → ∃xP(x) is true.
→ If P(x) is true for at least one element in the domain, then ∃xP(x) is true. Otherwise it is false.
→ Accordingly DeMorgan’s laws for quantifiers:the following statements are true.
¬∀xP(x) ≡ ∃x¬P(x)
¬∃xP(x) ≡ ∀x¬P(x) then the statement is ∃!x ⌐P(x) →⌐∀xP(x) is true. “Incorrect
“From the given question, → The symbol ∃ is call the existential quantifier and represents the phrase “there exists” or “for some”. The existential quantification of P(x) is the statement “P(x) for some values x in the universe”, or equivalently, “There exists a value for x such that P(x) is true”, which is written ∃xP(x). So the statement ∃!xP(x) → ∃xP(x) is true.
→ If P(x) is true for at least one element in the domain, then ∃xP(x) is true. Otherwise it is false.
→ Accordingly DeMorgan’s laws for quantifiers:the following statements are true.
¬∀xP(x) ≡ ∃x¬P(x)
¬∃xP(x) ≡ ∀x¬P(x) then the statement is ∃!x ⌐P(x) →⌐∀xP(x) is true. “ -
Question 5 of 30
5. Question
2 pointsWhich of the following shall be a compound proposition involving the propositions p, q and r, that is true when exactly two of the p, q and r are true and is false otherwise निम्नलिखित में से कौन सा एक प्रस्ताव प्रस्ताव होगा जिसमें प्रस्ताव p, q और r शामिल होगा, यह तब सच है जब p, q और r में से दो सही हों और अन्यथा गलत हों
Correct
“From the question, the propositions consists of exactly two of the variables should true and final proposition should be true.
Only option C consists of exactly two of the variables are true and all remaining variables deviating this rule.
In this proposition, (p ∧ q ∧⌐ r) ∨ ( p ∧ ⌐q ∧ r) ∨ (⌐ p ∧ q ∧ r)
(p ∧ q ∧⌐ r) → p and q are true
( p ∧ ⌐q ∧ r) → p and r are true
(⌐ p ∧ q ∧ r) → q and r are true
Finally the proposition consists of “V” operation , so the entire proposition is true. “Incorrect
“From the question, the propositions consists of exactly two of the variables should true and final proposition should be true.
Only option C consists of exactly two of the variables are true and all remaining variables deviating this rule.
In this proposition, (p ∧ q ∧⌐ r) ∨ ( p ∧ ⌐q ∧ r) ∨ (⌐ p ∧ q ∧ r)
(p ∧ q ∧⌐ r) → p and q are true
( p ∧ ⌐q ∧ r) → p and r are true
(⌐ p ∧ q ∧ r) → q and r are true
Finally the proposition consists of “V” operation , so the entire proposition is true. “ -
Question 6 of 30
6. Question
2 pointsHow many edges must be removed to produce the spanning forest of a graph with N vertices, M edges and C connected components ? एन कोने, एम किनारों और सी जुड़े घटकों के साथ ग्राफ के फैले जंगल का उत्पादन करने के लिए कितने किनारों को हटाया जाना चाहिए?
Correct
 Incorrect
Incorrect

-
Question 7 of 30
7. Question
2 pointsA test contains 100 true/false questions. How many different ways can a student answer the questions on the test, if the answer may be left blank also. एक परीक्षण में 100 सच्चे / झूठे प्रश्न होते हैं। विद्यार्थी परीक्षा में प्रश्नों के कितने अलग-अलग तरीके से उत्तर दे सकता है, यदि उत्तर को खाली भी छोड़ा जा सकता है।
Correct
 Incorrect
Incorrect

-
Question 8 of 30
8. Question
2 pointsThe relation “divides” on a set of positive integers is ________. सकारात्मक पूर्णांक के एक सेट पर “विभाजन” संबंध ________ है।
Correct
“The relation “divides” on a set of positive integers is Anti symmetric and Transitive.
Proof:
Let assume a,b two set elements.
The relation is antisymmetric if and only if for every a,b in the set.
IF(a∣b AND b∣a), then it must follow that a=b.
→ If it’s FALSE then both a∣b AND b∣a, then it’s perfectly consistent to have a≠b.
→ The only time a∣b AND b∣a is exactly when a=b, since then we have a∣b ⟺ a∣a is TRUE for all a.
Hence the relation is antisymmetric. “Incorrect
“The relation “divides” on a set of positive integers is Anti symmetric and Transitive.
Proof:
Let assume a,b two set elements.
The relation is antisymmetric if and only if for every a,b in the set.
IF(a∣b AND b∣a), then it must follow that a=b.
→ If it’s FALSE then both a∣b AND b∣a, then it’s perfectly consistent to have a≠b.
→ The only time a∣b AND b∣a is exactly when a=b, since then we have a∣b ⟺ a∣a is TRUE for all a.
Hence the relation is antisymmetric. “ -
Question 9 of 30
9. Question
2 points“Cyclometric complexity of a flow graph G with n vertices and e edges is
“”एन कोने और ई किनारों के साथ एक प्रवाह ग्राफ जी का साइक्लोमैटिक जटिलता है”Correct
“Cyclomatic complexity uses 3 formulas:
1. The number of regions corresponds to the cyclomatic complexity
2. V(G),Flow graph is defined as V(G)=E-N+2 where E is the number of flow graph edges, and N is the number of flow graph nodes.
3. V(G),Flow graph is defined as V(G)=P+1 where p is the number of predicate nodes contained in the flow graph G. “Incorrect
“Cyclomatic complexity uses 3 formulas:
1. The number of regions corresponds to the cyclomatic complexity
2. V(G),Flow graph is defined as V(G)=E-N+2 where E is the number of flow graph edges, and N is the number of flow graph nodes.
3. V(G),Flow graph is defined as V(G)=P+1 where p is the number of predicate nodes contained in the flow graph G. “ -
Question 10 of 30
10. Question
2 points“The proposition ~p ∨ q is equivalent to
प्रस्ताव ~ p is q के बराबर है”Correct
Draw the truth table and A is the answer. Its a very simple question.
Incorrect
Draw the truth table and A is the answer. Its a very simple question.
-
Question 11 of 30
11. Question
2 points“Any integer composed of 3n identical digits divisible by
3n समरूप अंकों से बना कोई भी पूर्णांक विभाज्य है”Correct
“Identical digits means similar(same) digits.
Any integer composed of 3n identical digits.
For example n=1, 3n= 31=3 which means three identical digits (111,222,333,444 and so on)
n=2, 32 =9 which means nine identical digits (111111111, 222222222 and so on)
The above numbers are is divisible by 3
111 is divisible by 3.
222, 333 and 444 are multiple of 3 “Incorrect
“Identical digits means similar(same) digits.
Any integer composed of 3n identical digits.
For example n=1, 3n= 31=3 which means three identical digits (111,222,333,444 and so on)
n=2, 32 =9 which means nine identical digits (111111111, 222222222 and so on)
The above numbers are is divisible by 3
111 is divisible by 3.
222, 333 and 444 are multiple of 3 “ -
Question 12 of 30
12. Question
2 pointsWhat is the probability of choosing correctly an unknown integer between 0 and 9 with 3 chances ? 3 अवसरों के साथ 0 और 9 के बीच एक अज्ञात पूर्णांक को सही ढंग से चुनने की संभावना क्या है?
Correct
“Probability of getting a number = 1/10
Probability of not getting a number = 1- 1/(10) = 9/10
Now probability that correct number is chosen in first chance= 1/10
probability that correct number is chosen in second chance= (9/10)* (1/10)
probability that correct number is chosen in first chance= (9/10)* (9/10) *(1/10)
So total probability = (1/10)+ [(9/10)* (1/10) ]+ [(9/10)* (9/10) *(1/10)]
= (1/10)+(9/100)+(81/1000)
= 271/1000, Hence none of the above “Incorrect
“Probability of getting a number = 1/10
Probability of not getting a number = 1- 1/(10) = 9/10
Now probability that correct number is chosen in first chance= 1/10
probability that correct number is chosen in second chance= (9/10)* (1/10)
probability that correct number is chosen in first chance= (9/10)* (9/10) *(1/10)
So total probability = (1/10)+ [(9/10)* (1/10) ]+ [(9/10)* (9/10) *(1/10)]
= (1/10)+(9/100)+(81/1000)
= 271/1000, Hence none of the above “ -
Question 13 of 30
13. Question
2 pointsThe proposition ~qvp is equivalent to प्रस्ताव ~ qvp के बराबर है
Correct
Draw the truth table
Incorrect
Draw the truth table
-
Question 14 of 30
14. Question
2 pointsA hash table has space for 75 records, then the probability of collision before the table is 6% full. एक हैश तालिका में 75 रिकॉर्ड के लिए जगह है, फिर तालिका से पहले टकराव की संभावना 6% भरी हुई है।
Correct
“Given data,
— Hash table has space =75 slots.
— For 6% filling it must take =6 slots.
— Probability of no collision for first 6 entries=?
Step-1: According to given data,
= (75P6) / (756)
= 0.814586387
Step-2: We have to find at least one collision occurs in 6 entries
=1-Probability of no collision for first 6 entries
= 1-0.814586387
= 0.185413613 , Hence none of the above “Incorrect
“Given data,
— Hash table has space =75 slots.
— For 6% filling it must take =6 slots.
— Probability of no collision for first 6 entries=?
Step-1: According to given data,
= (75P6) / (756)
= 0.814586387
Step-2: We have to find at least one collision occurs in 6 entries
=1-Probability of no collision for first 6 entries
= 1-0.814586387
= 0.185413613 , Hence none of the above “ -
Question 15 of 30
15. Question
2 pointsMaximum number of edges in a n-Node undirected graph without self loop is स्व-लूप के बिना एन-नोड अप्रत्यक्ष ग्राफ में किनारों की अधिकतम संख्या है
Correct
The set of vertices has size n, the number of such subsets is given by the binomial coefficient C(n,2)⋅C(n,2) = n(n-1)/2
Incorrect
The set of vertices has size n, the number of such subsets is given by the binomial coefficient C(n,2)⋅C(n,2) = n(n-1)/2
-
Question 16 of 30
16. Question
2 pointsThe number of colours required to properly colour the vertices of every planar graph is हर प्लानर ग्राफ के कोने को ठीक से रंगने के लिए आवश्यक रंगों की संख्या है
Correct
“→ The 4-colour theorem of the planar graph describes that any planar can at most be colored with 4 colors.
→ The sufficient number of colors in worst case is 4 colors for any planar graph. “Incorrect
“→ The 4-colour theorem of the planar graph describes that any planar can at most be colored with 4 colors.
→ The sufficient number of colors in worst case is 4 colors for any planar graph. “ -
Question 17 of 30
17. Question
2 pointsWhich of the following is an equivalence relation on the set of all functions from Z to Z ?
Correct
“An equivalence relation is a binary relation that is reflexive, symmetric and transitive.
The relation “”is equal to”” is the canonical example of an equivalence relation, where for any objects a, b, and c:
a = a (reflexive property),
if a = b then b = a (symmetric property), and
if a = b and b = c then a = c (transitive property)
“Incorrect
“An equivalence relation is a binary relation that is reflexive, symmetric and transitive.
The relation “”is equal to”” is the canonical example of an equivalence relation, where for any objects a, b, and c:
a = a (reflexive property),
if a = b then b = a (symmetric property), and
if a = b and b = c then a = c (transitive property)
“ -
Question 18 of 30
18. Question
2 pointsWhich of the relations on {0, 1, 2, 3} is an equivalence relation ?
Correct
“→ A relation on a set A is called an equivalence relation if it is reflexive, symmetric, and transitive.
1. Reflexivity: f(x) = f(x)
True, as given the same input, a function always produces the same output
2. Symmetry: if f(x) = f(y) then f(y) = f(x)
True, by the definition of equality
3.Transitivity: if f(x) = f(y) and f(y) = f(z) then f(x) = f(z)
True, by the definition of equality
Option-2: { (0,0), (1,1), (2,2), (3,3) }
Has all the properties, thus, is an equivalence relation
Option-1: { (0,0), (0,2), (2,0), (2,2), (2,3), (3,2), (3,3) }
Not reflexive: (1,1) is missing
Not transitive: (0,2) and (2,3) are in the relation, but not (0,3)
Option-3: { (0,0), (0,1) (0,2), (1,0), (1,1), (1,2), (2,0), (2,2), (3,3) }
Not symmetric: (1,2) is present, but not (2,1)
Not transitive: (2,0) and (0,1) are in the relation, but not (2,1)
Option-4: Similarly, option-4 also not TRUE “Incorrect
“→ A relation on a set A is called an equivalence relation if it is reflexive, symmetric, and transitive.
1. Reflexivity: f(x) = f(x)
True, as given the same input, a function always produces the same output
2. Symmetry: if f(x) = f(y) then f(y) = f(x)
True, by the definition of equality
3.Transitivity: if f(x) = f(y) and f(y) = f(z) then f(x) = f(z)
True, by the definition of equality
Option-2: { (0,0), (1,1), (2,2), (3,3) }
Has all the properties, thus, is an equivalence relation
Option-1: { (0,0), (0,2), (2,0), (2,2), (2,3), (3,2), (3,3) }
Not reflexive: (1,1) is missing
Not transitive: (0,2) and (2,3) are in the relation, but not (0,3)
Option-3: { (0,0), (0,1) (0,2), (1,0), (1,1), (1,2), (2,0), (2,2), (3,3) }
Not symmetric: (1,2) is present, but not (2,1)
Not transitive: (2,0) and (0,1) are in the relation, but not (2,1)
Option-4: Similarly, option-4 also not TRUE “ -
Question 19 of 30
19. Question
2 points Correct
Correct
 Incorrect
Incorrect

-
Question 20 of 30
20. Question
2 points“Consider the vocabulary with only four propositions A,B,C and D. How many models are there for the following sentence?
( ⌐ A ∨ ⌐ B ∨ ⌐ C ∨ ⌐ D) “”केवल चार प्रस्तावों ए, बी, सी और डी के साथ शब्दावली पर विचार करें। निम्नलिखित वाक्य में कितने मॉडल हैं?
(⌐ ए ⌐ ⌐ बी ∨ ∨ सी ⌐ “”डी)”””Correct
Here, number of models is nothing but number of TRUEs in final statement. Draw the truth table and count the “True” values in final output
Incorrect
Here, number of models is nothing but number of TRUEs in final statement. Draw the truth table and count the “True” values in final output
-
Question 21 of 30
21. Question
2 pointsIf we define the functions f, g and h that map R into R by : f(x) = x 4 , g(x) = √ x 2 + 1 , h(x) = x 2 + 72, then the value of the composite functions ho(gof) and (hog)of are given as अगर हम फ़ंक्शन को g, h और उस मैप R से R में परिभाषित करते हैं: f (x) = x 4, g (x) =) x 2 + 1, h (x) = x 2 + 72, तब समग्र कार्यों का मान हो (gof) और (हॉग) के रूप में दिया जाता है
Correct
“Given f(x) = x 4 , g(x) = √ x 2 + 1 , h(x) = x 2 + 72
for, ho(gof)
gof=g(f(x))
=g(x 4 )
=√(x 8 +1)
ho(gof)=h(gof)
=h(√(x 8 +1))
=(√(x 8 +1) 2 +72
=x 8 +1+72
=x 8 +73
√ x 2 + 1 , h(x) = x 2 + 72
for, (hog)of,
hog=h(g(x))
=h(√(x 2 +1)
=(√(x 2 +1) 2 +72
=x 2 + 1+72
=x 2 +73
(hog)of=(hog)(f(x))
=(hog)(x 4 )
=(x 4 ) 2 +73
=x 8 +73Incorrect
“Given f(x) = x 4 , g(x) = √ x 2 + 1 , h(x) = x 2 + 72
for, ho(gof)
gof=g(f(x))
=g(x 4 )
=√(x 8 +1)
ho(gof)=h(gof)
=h(√(x 8 +1))
=(√(x 8 +1) 2 +72
=x 8 +1+72
=x 8 +73
√ x 2 + 1 , h(x) = x 2 + 72
for, (hog)of,
hog=h(g(x))
=h(√(x 2 +1)
=(√(x 2 +1) 2 +72
=x 2 + 1+72
=x 2 +73
(hog)of=(hog)(f(x))
=(hog)(x 4 )
=(x 4 ) 2 +73
=x 8 +73 -
Question 22 of 30
22. Question
2 pointsA computer program selects an integer in the set {k : 1 ≤ k ≤ 10,00,000} at random and prints out the result. This process is repeated 1 million times. What is the probability that the value k=1 appears in the printout at least once ? कंप्यूटर प्रोग्राम सेट में एक पूर्णांक का चयन करता है {k: 1 ≤ k 00,000 10,00,000} यादृच्छिक पर और परिणाम को प्रिंट करता है। इस प्रक्रिया को 1 मिलियन बार दोहराया जाता है। क्या संभावना है कि मूल्य k = 1 प्रिंटआउट में कम से कम एक बार दिखाई देता है?
Correct
“Probability that the value k=1 appears in the printout at least once is
1-p(x=0)
We will apply the formula of binomial distribution
1-( 1000000 C 0 (1/1000000) 0 * (999999/1000000) 10^6 )
=1-(1*1*0.367879)
=0.632121 “Incorrect
“Probability that the value k=1 appears in the printout at least once is
1-p(x=0)
We will apply the formula of binomial distribution
1-( 1000000 C 0 (1/1000000) 0 * (999999/1000000) 10^6 )
=1-(1*1*0.367879)
=0.632121 “ -
Question 23 of 30
23. Question
2 points Correct
Correct
“Option-A: It is not complete graph because it won’t have n(n-1)/2 edges.
Option-B: It is not Bipartite Graph because it takes more than 2 colours. Bipartite Graph have exactly 2 colours.
Option-C: Hamiltonian path is a path in an undirected or directed graph that visits each vertex exactly once. “Incorrect
“Option-A: It is not complete graph because it won’t have n(n-1)/2 edges.
Option-B: It is not Bipartite Graph because it takes more than 2 colours. Bipartite Graph have exactly 2 colours.
Option-C: Hamiltonian path is a path in an undirected or directed graph that visits each vertex exactly once. “ -
Question 24 of 30
24. Question
2 pointsA certain tree has two vertices of degree 4, one vertex of degree 3 and one vertex of degree 2. If the other vertices have degree 1, how many vertices are there in the graph ? एक निश्चित पेड़ में डिग्री 4 के दो वर्टीकल होते हैं, डिग्री 3 के एक वर्टेक्स और डिग्री के एक वर्टेक्स 2. यदि दूसरे कोने में डिग्री 1 है, तो ग्राफ में कितने वर्टिक्स हैं?
Correct
“Here, they are clearly mentioned that “certain tree”
The tree contain maximum n-1 edges. Here, ‘n’ is number of vertices.
→ According to the handshaking lemma “sum of degrees of all vertices=2|e|”.
→ Two vertices of degree 4, we can write into (2*4)
→ One vertex of degree 3, we can write into (1*3)
→ One vertex of degree 2, we can write into (1*2).
→ Other vertices(X) have degree 1, we can write into (X*1)
Step-1: (2*4)+(1*3)+(1*2)+(X*1)
=2(X+4-1) [Note: ‘X’ value is not given ]
X=7
Step-2: To find total number of vertices, we are adding X+4 because they already given 4 vertices.
=X+4
=7+4
=11 “Incorrect
“Here, they are clearly mentioned that “certain tree”
The tree contain maximum n-1 edges. Here, ‘n’ is number of vertices.
→ According to the handshaking lemma “sum of degrees of all vertices=2|e|”.
→ Two vertices of degree 4, we can write into (2*4)
→ One vertex of degree 3, we can write into (1*3)
→ One vertex of degree 2, we can write into (1*2).
→ Other vertices(X) have degree 1, we can write into (X*1)
Step-1: (2*4)+(1*3)+(1*2)+(X*1)
=2(X+4-1) [Note: ‘X’ value is not given ]
X=7
Step-2: To find total number of vertices, we are adding X+4 because they already given 4 vertices.
=X+4
=7+4
=11 “ -
Question 25 of 30
25. Question
2 pointsConsider a set A = {1, 2, 3, …….., 1000}. How many members of A shall be divisible by 3 or by 5 or by both 3 and 5 ?
Correct
“The above problem is in the form of (AUB) = (A)+(B)-(A∩B)
A=1000/3
B=1000/5
(A∩B)=66
(AUB)=467 “Incorrect
“The above problem is in the form of (AUB) = (A)+(B)-(A∩B)
A=1000/3
B=1000/5
(A∩B)=66
(AUB)=467 “ -
Question 26 of 30
26. Question
2 pointsLet A={ x | -1 < x < 1 }=B. The function f(x)=x/2 from A to B is : A = {x | -1
Correct
“→ A function f : X → Y is defined to be one-one (or injective), if the images of distinct elements of X under f are distinct, i.e., x1 , x2 ∈ X, f(x1) = f(x2) ⇒ x1=x2.
→ The possible value of “x” is 0 then
f(x1)=x1/2=0/2=0
f(x2)=x2/2=0/2=0
for x1 , x2 ∈ X, f(x1) = f(x2) ⇒ x1 = x2. “Incorrect
“→ A function f : X → Y is defined to be one-one (or injective), if the images of distinct elements of X under f are distinct, i.e., x1 , x2 ∈ X, f(x1) = f(x2) ⇒ x1=x2.
→ The possible value of “x” is 0 then
f(x1)=x1/2=0/2=0
f(x2)=x2/2=0/2=0
for x1 , x2 ∈ X, f(x1) = f(x2) ⇒ x1 = x2. “ -
Question 27 of 30
27. Question
2 pointsFor a complete graph with N vertices, the total number of spanning trees is given by :
Correct
If a graph is complete, total number of spanning trees are N N-2
Incorrect
If a graph is complete, total number of spanning trees are N N-2
-
Question 28 of 30
28. Question
2 pointsIf (a^2 −b^2 ) is a prime number where a and b ε N, then : यदि (^ 2 −b ^ 2) एक अभाज्य संख्या है जहाँ a और b then N है, तो:
Correct
“→ For any given numbers a and b which belongs to natural numbers , the options (A) and (D) are false
→ The set of natural numbers, denoted N, can be defined in the following ways: N = {0, 1, 2, 3, …}
→ A prime number (or a prime) is a natural number greater than 1 that cannot be formed by multiplying two smaller natural numbers.
→ ‘a-b’ may be gives the non negative values which is not prime number but the a+b may give the prime value. “Incorrect
“→ For any given numbers a and b which belongs to natural numbers , the options (A) and (D) are false
→ The set of natural numbers, denoted N, can be defined in the following ways: N = {0, 1, 2, 3, …}
→ A prime number (or a prime) is a natural number greater than 1 that cannot be formed by multiplying two smaller natural numbers.
→ ‘a-b’ may be gives the non negative values which is not prime number but the a+b may give the prime value. “ -
Question 29 of 30
29. Question
2 pointsMinimum number of individual shoes to be picked up from a dark room ( containing 10 pair of shoes) if we have to get at least one proper pair :
Correct
“→ There are 10 pair of shoes available in the dark room which means 20 individual shoes are available in the room.
→ If you pick shoes from one to ten individual shoes, there may be chance of getting same individual shoes.
→ There is no guarantee that getting one proper pair from 10 individual shoes.
→ If You pick 11 shoes, then there may chance of 10 individual shoes of same type and one individual shoe of another type. So we will get at least one proper pair shoe from 11 individual shoes. “Incorrect
“→ There are 10 pair of shoes available in the dark room which means 20 individual shoes are available in the room.
→ If you pick shoes from one to ten individual shoes, there may be chance of getting same individual shoes.
→ There is no guarantee that getting one proper pair from 10 individual shoes.
→ If You pick 11 shoes, then there may chance of 10 individual shoes of same type and one individual shoe of another type. So we will get at least one proper pair shoe from 11 individual shoes. “ -
Question 30 of 30
30. Question
2 pointsConsider the relation on the set of non-negative integers defined by x ≡ y if and only if यदि और केवल यदि x and y द्वारा परिभाषित गैर-नकारात्मक पूर्णांकों के सेट पर संबंध पर विचार करें
Correct
“A relation R is an equivalence relation if and only if it is reflexive, symmetric, and transitive.
1. The relation is reflexive: x mod 3 = x mod 3
2. The relation is symmetric: if x mod 3 = y mod 3, then y mod 3 = x mod 3
3. The relation is transitive: if x mod 3 = y mod 3, and y mod 3 = z mod 3, then x mod 3 = z mod 3 “Incorrect
“A relation R is an equivalence relation if and only if it is reflexive, symmetric, and transitive.
1. The relation is reflexive: x mod 3 = x mod 3
2. The relation is symmetric: if x mod 3 = y mod 3, then y mod 3 = x mod 3
3. The relation is transitive: if x mod 3 = y mod 3, and y mod 3 = z mod 3, then x mod 3 = z mod 3 “






